Question

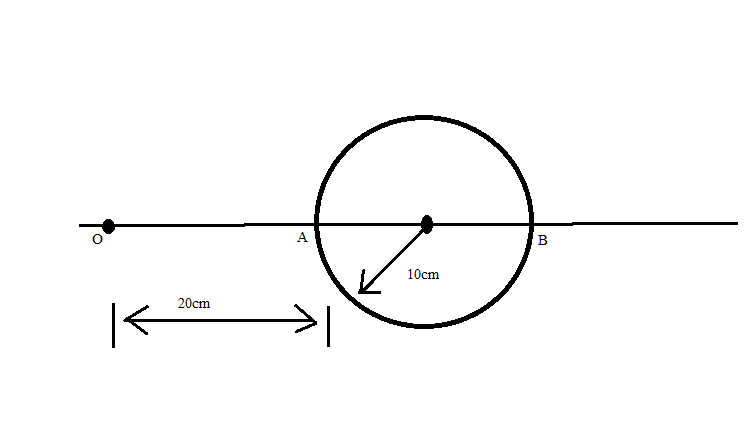
A glass sphere of radius $\text{R=10cm}$ is kept inside water. A point object O is displaced at $\text{20cm}$ from A as shown in figure. Find the position and nature of the image from the other side.
${{\mu }_{g}}=\dfrac{3}{2}and{{\mu }_{w}}=\dfrac{4}{3}$

Answer 1

Hint: The light ray coming from the point O will be refracted twice. The students can use the formula for refraction from a surface associated with the object distance and the image distance, so as to find the final position of the image formed.

Complete step-by-step answer:
If $\text{u}$is taken as the object distance and $\text{v }$is the image distance, and $\text{R}$ is the radius of curvature, then we can write as,
$\begin{align}
  & \dfrac{{{\mu }_{g}}}{v}-\dfrac{{{\mu }_{r}}}{u}=\dfrac{{{\mu }_{g}}-{{\mu }_{r}}}{R} \\
 & \Rightarrow \dfrac{3}{2v}-\dfrac{4}{3u}=\dfrac{\dfrac{3}{2}-\dfrac{4}{3}}{R} \\
 & \Rightarrow \dfrac{3}{2v}-\dfrac{4}{3u}=\dfrac{1}{6R} \\
\end{align}$
Now according to the given question, for the first refracting surface,
$u=-20cm\text{ and }v=+10cm\text{ and }R=+10cm$
Therefore, the above equation will give us the result as,
$\begin{align}
  & \dfrac{3}{2v}-\dfrac{4}{3u}=\dfrac{1}{6R} \\
 & \Rightarrow \dfrac{3}{2v}-\dfrac{4}{3(-20)}=\dfrac{1}{6(10)} \\
 & \Rightarrow v=-30cm \\
 & \\
\end{align}$
That is, the image formed is virtual.
Therefore, the new object distance for the second refracting surface will be
$\begin{align}
  & u=(-20-30) \\
 & \Rightarrow u=-50cm \\
\end{align}$
Again let us use the same formula in order to determine the final position of the image.
$u=-50cm\text{ and }v=-10cm\text{ and }R=-10cm$
Therefore, we get from the formula,
$\begin{align}
  & \dfrac{4}{3v}-\dfrac{3}{2(-50)}=\dfrac{1}{60} \\
 & \Rightarrow \dfrac{4}{3v}+\dfrac{3}{100}=\dfrac{1}{60} \\
 & \Rightarrow v=-100cm \\
\end{align}$
As the position of the final image has a negative sign , it means that the image formed will be virtual.
Therefore from the above calculations, we can conclude that the final image formed by the refracting surface will be virtual and it will be formed at a distance of 100cm from the surface.

Additional information:
The Refractive Index of a material is a dimensionless quantity which gives us a measure of how fast light travels in a particular medium. Refractive index of a medium also determines how much the path of light is bent, or refracted, when entering a material.

Note: Students must be careful while taking the signs of the position of the object and the image from the refracting surface. The radius of curvature in the first case was positive because the light rays were hitting the convex surface, but in the second case, they were hitting the concave surface.