Question

A garden is 90 m long and 75 m broad. A path 5 m wide is to be built outside and around it. Find the area of the path. Also find the area of the garden in hectares.

Answer 1

Hint: Here, we will find the area of the path by subtracting the inner area from the outer area of the garden.

Here the garden is in the shape of a rectangle.
Given,
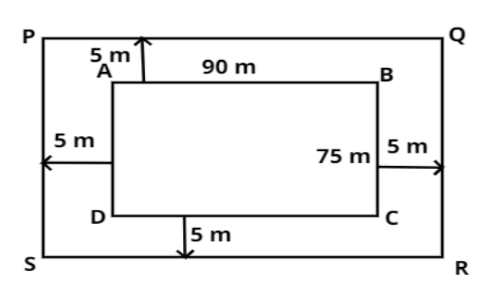
Inner length of the garden (AB) $l = 90$ m
Inner width of the garden (BC) $b = 75$ m
As we know that ${\text{Area of a rectangle}} = \left( {{\text{Length of the rectangle}}} \right) \times \left( {{\text{Width of the rectangle}}} \right)$
So, ${\text{Area of inner rectangle ABCD}} = l \times b = 90 \times 75 = 6750$ m2
According to the problem, a path of 5 m wide is to be built around this garden as shown in figure
Here, Outer length of the garden (PQ) $L = l + 5 + 5 = 90 + 5 + 5 = 100$ m
Outer width of the garden (QR) \[B = b + 5 + 5 = 75 + 5 + 5 = 85\] m
So, ${\text{Area of the outer rectangle PQRS}} = L \times B = 100 \times 85 = 8500$ m2
$
  {\text{Area of the path}} = {\text{Area of rectangle PQRS}} - {\text{Area of rectangle ABCD}} \\
   \Rightarrow {\text{Area of the path}} = 8500 - 6750 = 1750\,{{\text{m}}^2} \\
 $
Therefore, the area of the path is 1750 m2.
Since, we know that $1{\text{ hectare}} = 10000{\text{ }}{{\text{m}}^2}$
Also, ${\text{Area of the garden}} = {\text{Area of inner rectangular ABCD}} = 6750{\text{ }}{{\text{m}}^2} = \dfrac{{6750}}{{10000}} = 0.675{\text{ hectare}}$.
Therefore, the area of the garden in hectare is 0.675 hectare.

Note: In the above problem, when a path of 5 m wide is built, the outer dimensions are increased by 10 m in both x and y direction which is clearly visible from the figure.