
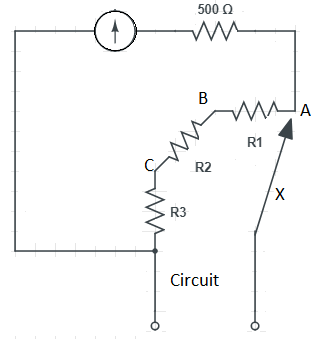
A galvanometer is used to measure the small currents. A certain galvanometer has a resistance of 500Ω and gives a full scale deflection for a current of 200μA. This meter is connected as shown in the figure to make a multi range current meter. Connections to the circuit are made at the terminal shown. The currents in the external circuit needed to give full scale deflection when X is connected to A, B and C in turn is shown in the table.
X connected to Current in the external circuit (mA) A 1 B 10 C 100
Find out the of ${{R}_{3}}$is
A. 2.25 Ω
B. 0.25 Ω
C. 1.25 Ω
D. 3.25Ω
| X connected to | Current in the external circuit (mA) |
| A | 1 |
| B | 10 |
| C | 100 |

Answer
570.3k+ views
Hint: In order to solve this question we have to use the Kirchhoff’s law for the give 3 conditions one by one which will give us combination of resistance by solving those equation we will get value of resistance ${{R}_{3}}$.
Formula used:
V=IR
Complete step by step solution:
Now in order to get the solution we have to apply given 3 conditions one by one.
Given data:
$\begin{align}
& R=500\Omega \\
& I=200\mu A \\
& =200\times {{10}^{-6}}A \\
& {{I}_{1}}=1mA \\
& =1\times {{10}^{-3}}A \\
& {{I}_{2}}=10mA \\
& =10\times {{10}^{-3}}A \\
& {{I}_{3}}=100mA \\
& =100\times {{10}^{-3}} \\
\end{align}$
Now condition (i) when X is connected to A.
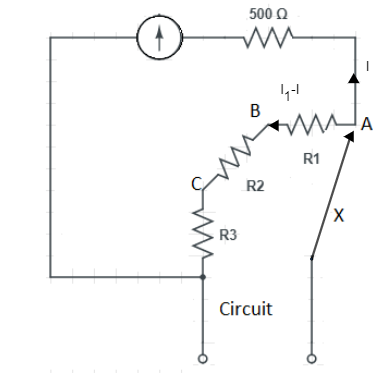
Now from the fig (i) let’s apply Kirchhoff’s law
$500\times I=\left( {{R}_{1}}+{{R}_{2}}+{{R}_{3}} \right)\times \left( {{I}_{1}}-I \right)$
Here all the three resistance are connected in the series therefore we can apply the series rule of the resistance.
Now let’s substitute all the values in the equation.
$\begin{align}
& \Rightarrow 500\times 200\times {{10}^{-6}}=\left( {{R}_{1}}+{{R}_{2}}+{{R}_{3}} \right)\times \left( 1\times {{10}^{-3}}-200\times {{10}^{-6}} \right) \\
& \Rightarrow {{R}_{1}}+{{R}_{2}}+{{R}_{3}}=\dfrac{500\times 200\times {{10}^{-6}}}{0.8\times {{10}^{-3}}} \\
& \Rightarrow {{R}_{1}}+{{R}_{2}}+{{R}_{3}}=\dfrac{10\times {{10}^{4}}\times {{10}^{-6}}\times {{10}^{3}}}{0.8} \\
& \Rightarrow {{R}_{1}}+{{R}_{2}}+{{R}_{3}}=125 \\
& \therefore {{R}_{1}}+{{R}_{2}}=125-{{R}_{3}}....\left( 1 \right) \\
\end{align}$
Now let’s apply the second condition:
When X is connected to the point B, circuit will becomes as shown in the figure (i)
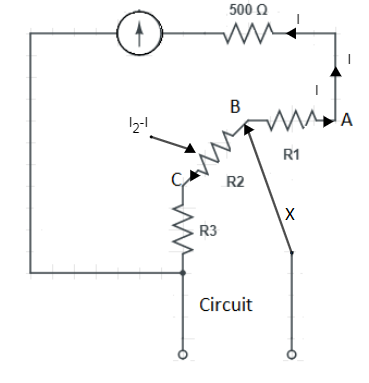
Now let’s apply Kirchhoff’s law in the circuit shown in the figure (ii)
\[\begin{align}
& \Rightarrow \left( 500+{{R}_{1}} \right)I=\left( {{R}_{2}}+{{R}_{3}} \right)\times \left( {{I}_{2}}-I \right) \\
& \Rightarrow \left( 500+{{R}_{1}} \right)\times 200\times {{10}^{-6}}=\left( {{R}_{2}}+{{R}_{3}} \right)\times \left( 10\times {{10}^{-3}}-200\times {{10}^{-6}} \right) \\
& \Rightarrow \left( 500+{{R}_{1}} \right)=\dfrac{\left( {{R}_{2}}+{{R}_{3}} \right)\times 9.8\times {{10}^{-3}}}{200\times {{10}^{-6}}} \\
& \therefore \left( 500+{{R}_{1}} \right)=49\left( {{R}_{2}}+{{R}_{3}} \right)....\left( 2 \right) \\
\end{align}\]
Now let’s apply third condition:
When X is connected to the point C our circuit will be,
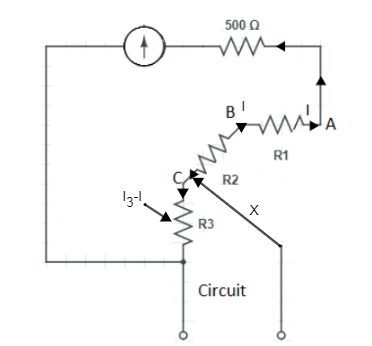
Now let’s apply Kirchhoff’s law on circuit shown in the figure (iii)
$\begin{align}
& \Rightarrow \left( 500+{{R}_{1}}+{{R}_{2}} \right)\times I={{R}_{3}}\times \left( {{I}_{3}}-I \right) \\
& \Rightarrow \left( 500+{{R}_{1}}+{{R}_{2}} \right)\times 200\times {{10}^{-6}}={{R}_{3}}\left( 100\times {{10}^{-3}}-200\times {{10}^{-6}} \right) \\
& \Rightarrow 500+{{R}_{1}}+{{R}_{2}}=\dfrac{{{R}_{3}}\times 99.8\times {{10}^{-3}}}{200\times {{10}^{-6}}} \\
& \therefore 500+{{R}_{1}}+{{R}_{2}}={{R}_{3}}\times 499...\left( 3 \right) \\
\end{align}$
Now from the equation (1) substitute value of the $\left( {{R}_{1}}+{{R}_{2}} \right)$ in the equation (3)
$\begin{align}
& \Rightarrow 500+125-{{R}_{3}}=499{{R}_{3}} \\
& \Rightarrow 00{{R}_{3}}=625 \\
& \therefore {{R}_{3}}=1.25\Omega \\
\end{align}$
Hence, the option (c) is correct.
Note:
When we are dividing current be careful when putting $\left( {{I}_{1}}-I
\right)$ or $\left( {{I}_{2}}-I \right)$ or $\left( {{I}_{3}}-I \right)$ it can be
mistaken or misplaced as $\left( I-{{I}_{1}} \right)$ or $\left( I-{{I}_{2}}
\right)$ or $\left( I-{{I}_{3}} \right)$ which can lead us to the wrong answer.
Formula used:
V=IR
Complete step by step solution:
Now in order to get the solution we have to apply given 3 conditions one by one.
Given data:
$\begin{align}
& R=500\Omega \\
& I=200\mu A \\
& =200\times {{10}^{-6}}A \\
& {{I}_{1}}=1mA \\
& =1\times {{10}^{-3}}A \\
& {{I}_{2}}=10mA \\
& =10\times {{10}^{-3}}A \\
& {{I}_{3}}=100mA \\
& =100\times {{10}^{-3}} \\
\end{align}$
Now condition (i) when X is connected to A.

Now from the fig (i) let’s apply Kirchhoff’s law
$500\times I=\left( {{R}_{1}}+{{R}_{2}}+{{R}_{3}} \right)\times \left( {{I}_{1}}-I \right)$
Here all the three resistance are connected in the series therefore we can apply the series rule of the resistance.
Now let’s substitute all the values in the equation.
$\begin{align}
& \Rightarrow 500\times 200\times {{10}^{-6}}=\left( {{R}_{1}}+{{R}_{2}}+{{R}_{3}} \right)\times \left( 1\times {{10}^{-3}}-200\times {{10}^{-6}} \right) \\
& \Rightarrow {{R}_{1}}+{{R}_{2}}+{{R}_{3}}=\dfrac{500\times 200\times {{10}^{-6}}}{0.8\times {{10}^{-3}}} \\
& \Rightarrow {{R}_{1}}+{{R}_{2}}+{{R}_{3}}=\dfrac{10\times {{10}^{4}}\times {{10}^{-6}}\times {{10}^{3}}}{0.8} \\
& \Rightarrow {{R}_{1}}+{{R}_{2}}+{{R}_{3}}=125 \\
& \therefore {{R}_{1}}+{{R}_{2}}=125-{{R}_{3}}....\left( 1 \right) \\
\end{align}$
Now let’s apply the second condition:
When X is connected to the point B, circuit will becomes as shown in the figure (i)

Now let’s apply Kirchhoff’s law in the circuit shown in the figure (ii)
\[\begin{align}
& \Rightarrow \left( 500+{{R}_{1}} \right)I=\left( {{R}_{2}}+{{R}_{3}} \right)\times \left( {{I}_{2}}-I \right) \\
& \Rightarrow \left( 500+{{R}_{1}} \right)\times 200\times {{10}^{-6}}=\left( {{R}_{2}}+{{R}_{3}} \right)\times \left( 10\times {{10}^{-3}}-200\times {{10}^{-6}} \right) \\
& \Rightarrow \left( 500+{{R}_{1}} \right)=\dfrac{\left( {{R}_{2}}+{{R}_{3}} \right)\times 9.8\times {{10}^{-3}}}{200\times {{10}^{-6}}} \\
& \therefore \left( 500+{{R}_{1}} \right)=49\left( {{R}_{2}}+{{R}_{3}} \right)....\left( 2 \right) \\
\end{align}\]
Now let’s apply third condition:
When X is connected to the point C our circuit will be,

Now let’s apply Kirchhoff’s law on circuit shown in the figure (iii)
$\begin{align}
& \Rightarrow \left( 500+{{R}_{1}}+{{R}_{2}} \right)\times I={{R}_{3}}\times \left( {{I}_{3}}-I \right) \\
& \Rightarrow \left( 500+{{R}_{1}}+{{R}_{2}} \right)\times 200\times {{10}^{-6}}={{R}_{3}}\left( 100\times {{10}^{-3}}-200\times {{10}^{-6}} \right) \\
& \Rightarrow 500+{{R}_{1}}+{{R}_{2}}=\dfrac{{{R}_{3}}\times 99.8\times {{10}^{-3}}}{200\times {{10}^{-6}}} \\
& \therefore 500+{{R}_{1}}+{{R}_{2}}={{R}_{3}}\times 499...\left( 3 \right) \\
\end{align}$
Now from the equation (1) substitute value of the $\left( {{R}_{1}}+{{R}_{2}} \right)$ in the equation (3)
$\begin{align}
& \Rightarrow 500+125-{{R}_{3}}=499{{R}_{3}} \\
& \Rightarrow 00{{R}_{3}}=625 \\
& \therefore {{R}_{3}}=1.25\Omega \\
\end{align}$
Hence, the option (c) is correct.
Note:
When we are dividing current be careful when putting $\left( {{I}_{1}}-I
\right)$ or $\left( {{I}_{2}}-I \right)$ or $\left( {{I}_{3}}-I \right)$ it can be
mistaken or misplaced as $\left( I-{{I}_{1}} \right)$ or $\left( I-{{I}_{2}}
\right)$ or $\left( I-{{I}_{3}} \right)$ which can lead us to the wrong answer.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Draw ray diagrams each showing i myopic eye and ii class 12 physics CBSE

Give 10 examples of unisexual and bisexual flowers

Give simple chemical tests to distinguish between the class 12 chemistry CBSE

Define Vant Hoff factor How is it related to the degree class 12 chemistry CBSE




