Question

A flagpole stands on a building of height \[450{\text{ }}ft\] and an observer on level ground is \[300{\text{ }}ft\] from the base of the building . The angle of elevation of the bottom of the flagpole is \[30^\circ \] and the height of the flagpole is \[50{\text{ }}ft\] . If \[\theta \] is the angle of elevation of the top of the flagpole , then \[\tan \theta \] is
\[\left( 1 \right)\] \[\dfrac{4}{{3\sqrt 3 }}\]
\[\left( 2 \right)\] \[\dfrac{{\sqrt 3 }}{2}\]
\[\left( 3 \right)\] \[\dfrac{9}{2}\]
\[\left( 4 \right)\] \[\dfrac{{\sqrt 3 }}{5}\]
\[\left( 5 \right)\] \[\dfrac{{4\sqrt 3 + 1}}{6}\]

Answer 1

Hint: We have to find the value of \[\tan \theta \] in the given problem . We solve this question using the concept of applications of trigonometry . We should have the knowledge of the basic trigonometric functions and their values . We would construct a diagram for a reference and using the various relations of trigonometry and using the values of trigonometric functions we will find the value of \[\tan \theta \].

Complete answer: Given :
A flagpole stands on a building of height \[450{\text{ }}ft\] and an observer on level ground is \[300{\text{ }}ft\] from the base of the building . The angle of elevation of the bottom of the flagpole is \[30^\circ \] and the height of the flagpole is \[50{\text{ }}ft\] . \[\theta \] is the angle of elevation of the top of the flagpole .
Construct : According to the question , we construct a diagram as shown .

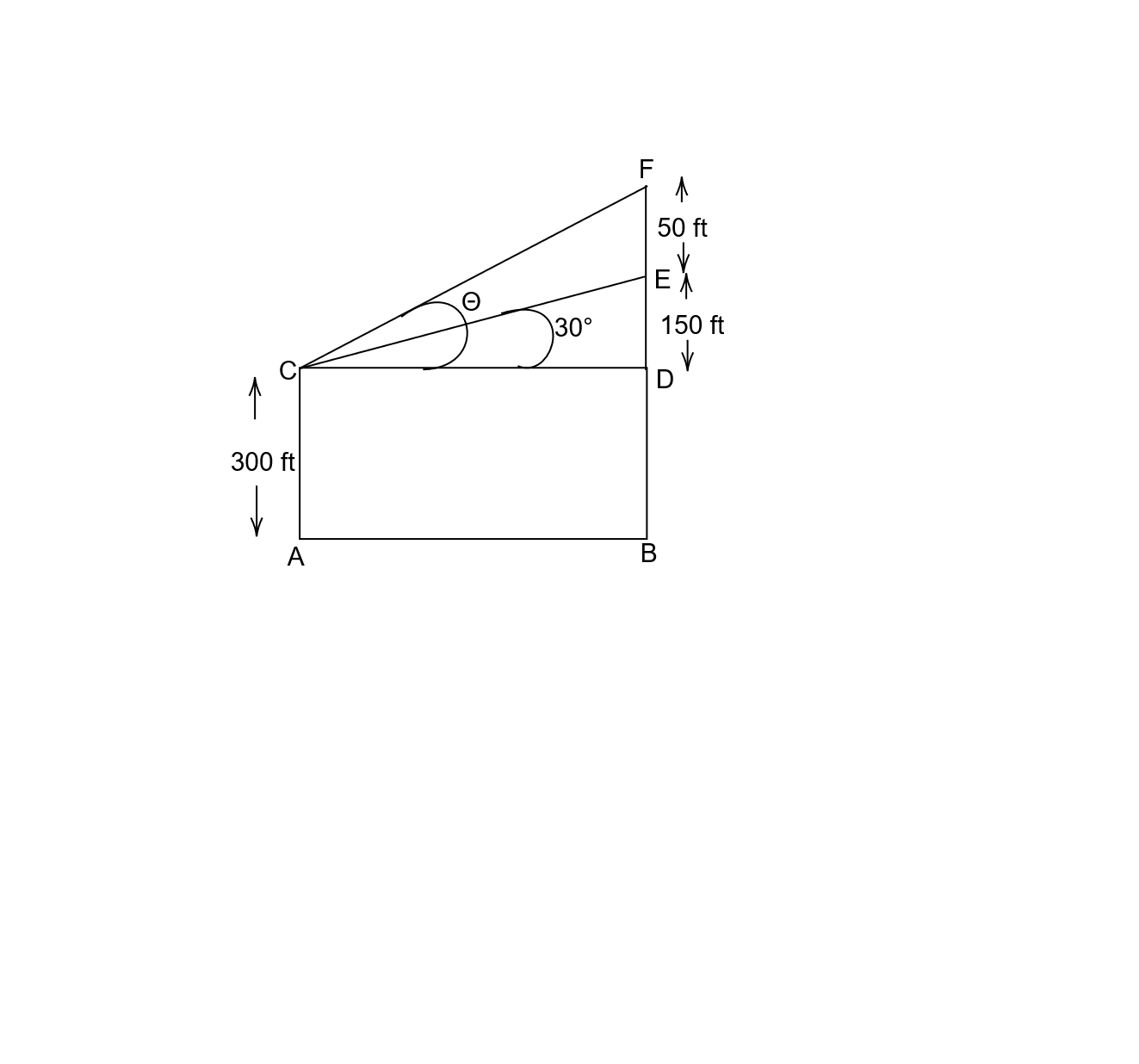
Now ,
In triangle \[DCE\] ,
\[\tan {30^ \circ } = \dfrac{{DE}}{{DC}}\]
[As we know that \[tan{\text{ }}x{\text{ }} = {\text{ }}\dfrac{{perpendicular}}{{base}}\]]
As , we know that \[\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}\]
We get ,
\[\dfrac{1}{{\sqrt 3 }} = \dfrac{{DE}}{{DC}}\]
\[CD = \sqrt 3 \times DE\]
And , \[DE{\text{ }} = {\text{ }}150\]
So ,
\[CD = 150\sqrt 3 - - - (1)\]
In triangle \[DCF\] ,
\[\tan \theta = \dfrac{{FD}}{{CD}}\]
\[\left[ {FD{\text{ }} = {\text{ }}150{\text{ }} + {\text{ }}50{\text{ }} = {\text{ }}200} \right]\]
\[\tan \theta = \dfrac{{200}}{{150\sqrt 3 }}\]
Cancelling the terms , we get
\[\tan \theta = \dfrac{4}{{3\sqrt 3 }}\]
Thus , the value of \[\tan \theta \] is \[\dfrac{4}{{3\sqrt 3 }}\] .
Hence , the correct option is \[\left( 1 \right)\] .

Note:
Applications of trigonometry : It is the property or the concept of trigonometry which can be used in our daily life to either find the length or the angle of elevations of a body , building , the length of the formation of shadow of an object due to light . We can also compute the value or the measurement for the depth in the river of an object above it . This can also help us in finding the speed of an object moving in a direction which is seen by a person sitting on a height .