Question

A fighter plane is moving in a vertical circle of radius 'r'. Its minimum velocity at the highest point A of the circle will be:

A. $\sqrt{3gr}$
B. $\sqrt{2gr}$
C. $\sqrt{gr}$
D. $\sqrt{gr/2}$

Answer 1

Hint: We will first draw the free body diagram of the fighter plane as per the given conditions and then at its highest point we will equate the forces acting on it, we will notice that two forces are acting on the fighter plane in two directions. One towards the earth that is the gravitational pull and another force acting towards the opposite direction counterbalancing the gravitational pull.

Complete step by step answer:

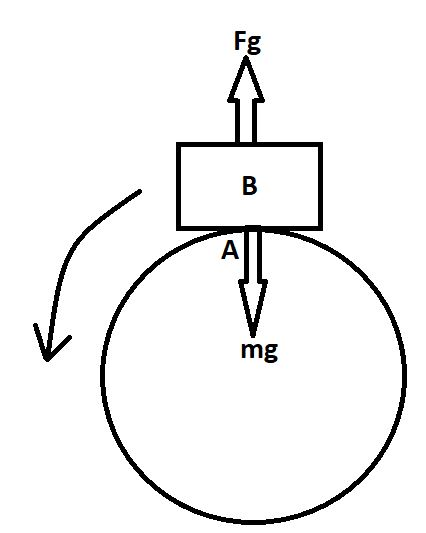
Here in the above diagram we see, the fighter plane B is at the top of the circle that is at point A.
Now, the arrow indicates the direction of the fighter plane, and there are two forces working on the airplane when it is at the top position, which is at point A. These two forces are counterbalancing each other and stop the fighter plane from falling down.

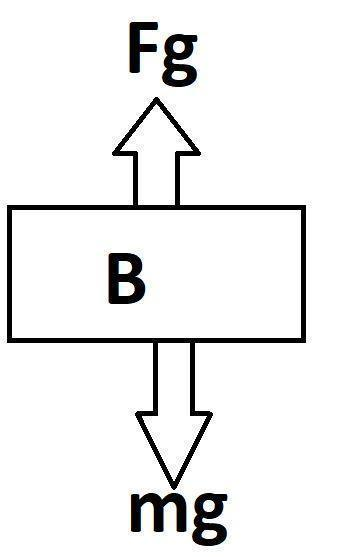
And this diagram is the free body diagram of that plane in its highest position.
Now, according to the problem
we know that, for a moving object in a circle of radius ‘r’,
At the highest point, the weight of the fighter plane will act downwards and so in order to keep the plane in motion and in the trajectory, another force acting upward should be balancing it. Let us take this force as $F_g$ which is equal to
$F_g$ = $\dfrac{m{{v}^{2}}}{r}$ ,
Now, according to the problem
 mg $\le $$\dfrac{m{{v}^{2}}}{r}$,
Here the m cancels out, and
g $\le $$\dfrac{{{v}^{2}}}{r}$,
gr $\le $${{v}^{2}}$,
$\sqrt{gr}\le v$ ,
We had to find the minimum velocity at point A, hence
$v = \sqrt{gr}$
Therefore option C is the correct option.

Note:
Try to figure out the forces acting on the body properly as it is the most important step of the answer, $F_g$ that is the force counterfeiting the force of gravitation is the greater force because without that force the fighter plane will simply fall down, when we got the answer it was in the relation of greater than equals to but we need it in equals to form so we are considering it as equals to because in the question it was written to get the minimum velocity.