Question

A fighter plane flying horizontally at an altitude of \[1.5km\] with speed $720km/h$ passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed $600ms^{-1}$ to hit the plane? At what minimum altitude should the pilot fly the plane to avoid being hit? (Take $g=10ms^{-2}$)

Answer 1

Hint: This can be solved by the projectile motion where $u \sin\theta=vt$. Since the plane is already at certain height above the ground, we must check, the max height, till where the shell can reach $H_{max}=\dfrac{u^{2}sin^{2}(90-\theta)}{2g}$.

Formula used: $u \sin\theta=vt$
$H_{max}=\dfrac{u^{2}sin^{2}(90-\theta)}{2g}$

Complete step-by-step solution -
This is a projectile motion sum where,
Height of the fighter plane=$1.5km=1500m$
Speed of the plane $v=720km/h=200m/s$
Let $\theta$ be the angle, when the shell hits the plane.
Muzzle velocity $u=600m/s$
Time taken to hit the plane$=t$
Horizontal distance travelled, from second equation of kinematic motion.$=u_{x}t$
Distance travelled by the plane$=vt$

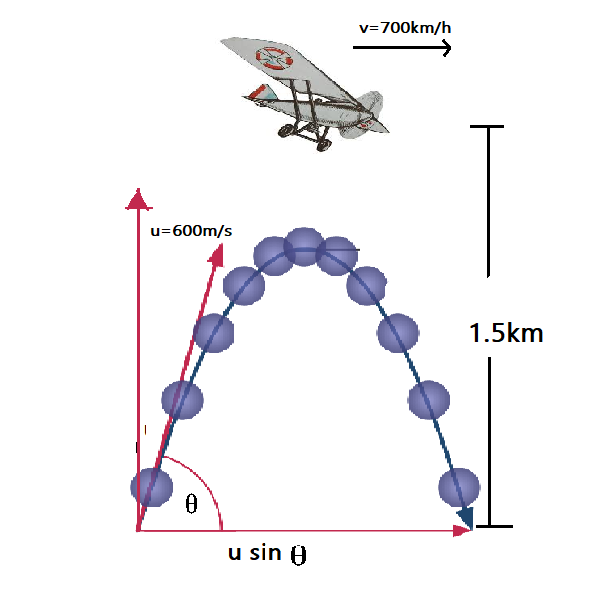
The shell will hit the plane if the above distances are equal.
$u_{x}t=vt$
$u \sin\theta=vt$
$\sin \theta=\dfrac{u}{v}=\dfrac{200}{600}=0.33$
$\theta=\sin^{-1}(0.33)\approx19^{\circ}$
To avoid being hit, the plane must fly at $H_{max}=\dfrac{u^{2}sin^{2}(90-\theta)}{2g}=\dfrac{u^{2}cos^{2}\theta}{2\times10}=\dfrac{600^{2}cos^{2}19}{20}=\dfrac{(600\times0.945)^{2}}{20}=16092=16km$
Since it is already flying at \[1.5km\] height it must fly above by another \[16km\] to avoid being hit by the shell.

Note: Projectile motion occurs when an object is projected at a certain angle from the surface, it moves along a curved path called trajectory under the action of gravity. This curved path is of the shape of a parabola.
The various formulas used are
Time of flight$=\dfrac{2v_{0}\sin\theta}{g}$
Maximum height $H_{max}=\dfrac{u^{2}sin^{2}(90-\theta)}{2g}$
Horizontal range $R=\dfrac{u^{2}sin^{2}(90-\theta)}{g}$
Where, $v_{0}$ is the initial velocity, with $\sin\theta\;;\cos\theta$ as the y-axis and x-axis component respectively.