Question

A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand-operated. It takes 4 minutes on the automatic and 6 minutes on hand-operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand-operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs.7 and screws B at a profit of Rs.10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.

Answer 1

Hint:
Here we will firstly find the constraint equations from the data given in the question. Then we will find the objective function for maximizing the profit. We will plot the constraints in the graph and find the corner points. Then we will check at which corner point the objective function is maximum.

Complete step by step solution:
Let \[X\] be the number of packages manufactured of screws A and \[Y\] be the number of packages manufactured of screws B.
Now we will make the conditional statements from the data given in the question.
It is given that it takes 4 minutes on the automatic to manufacture a package of screws A and it takes 6 minutes on automatic to manufacture a package of screws B also it is given that each machine is available for at the most 4 hours or 240 minutes on any day.
Therefore the equation is \[4X + 6Y \le 240\].
Now dividing both sides by 2, we get
\[ \Rightarrow 2X + 3Y \le 120\]…………………….\[\left( 1 \right)\]
As it takes 6 minutes on hand-operated machines to produce a package of screws A and 3 minutes on the hand-operated machines to produce a package of screws B. It is given that each machine is only available for at the most 4 hours or we can say 240 minutes on any day.
Therefore the equation is \[6X + 3Y \le 240\]
Now dividing both sides by 3, we get
\[ \Rightarrow 2X + Y \le 80\]…………………….\[\left( 2 \right)\]
Also we know that the quantity of the packages manufactured cannot be negative. Therefore
\[X \ge 0\]…………………….\[\left( 3 \right)\]
And
\[Y \ge 0\]…………………..\[\left( 4 \right)\]
Now we have to make the objective function of the equation. As we have to maximize the profit. It is given that the manufacturer can sell a package of screws A at a profit of Rs.7 and screws B at a profit of Rs.10.
Therefore, the objective function is \[Z = 7X + 10Y\].
Now we have to plot all the equations constraints from the equation \[\left( 1 \right)\], \[\left( 2 \right)\], \[\left( 3 \right)\] and \[\left( 4 \right)\] in the graph to get the feasible region.

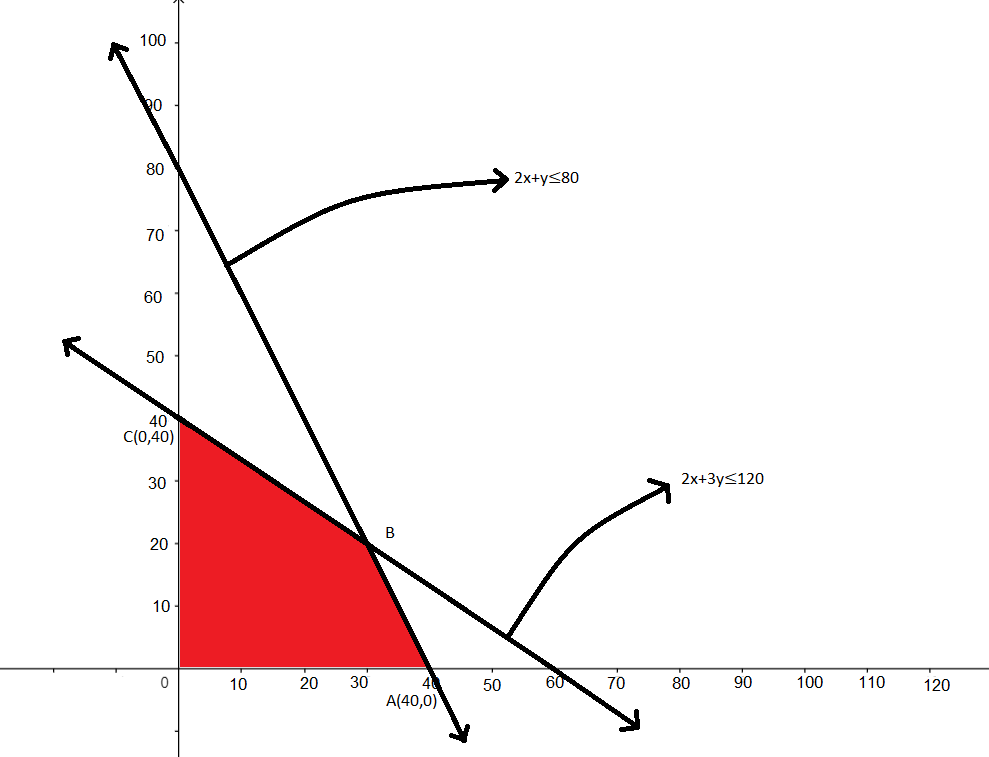
Now, we will find corner point B by solving the equation \[\left( 1 \right)\] and \[\left( 2 \right)\]. So we get coordinates of point B as \[\left( {30,20} \right)\].
Hence, there are three corner points of the feasible region i.e. \[A\left( {40,0} \right),B\left( {30,20} \right),C\left( {0,40} \right)\].
Now, we will find the value of the objective function at every corner point and find that corner point at which the objective function is maximum. Therefore, we get
Objective function at corner point \[A\left( {40,0} \right)\] is
\[Z = 7 \times 40 + 10 \times 0 = 280\]
Objective function at corner point \[B\left( {30,20} \right)\] is
\[Z = 7 \times 30 + 10 \times 20 = 210 + 200 = 410\]
Objective function at corner point \[C\left( {0,40} \right)\] is
\[Z = 7 \times 0 + 10 \times 40 = 400\]
So, we can clearly see that the objective function is maximum at corner point \[B\left( {30,20} \right)\] i.e. at \[X = 30\] and \[Y = 20\].
Hence, the factory owner should manufacture \[30\] packages of the screw A and manufacture \[20\] packages of the screw B to maximize the profit.

Hence, the maximum profit is Rs. 410.

Note:
Here we have to note that the constraints equation should be formed carefully. While forming the equations we have to convert the total time of working into the minutes as it is given in hours. Also, we have to note that we cannot take the origin as the corner point, if we take origin as a corner point, then the value of objective function will be zero.
Feasible region is the search space or the solution space where the value of the objective function is optimal. Maximum and the minimum value of the objective function are generally at the corner points of the feasible region.