Question

A factory makes cricket bats and hockey sticks. A bat takes 1.5 hour of machine time and 2 hours of craftsman time. While a hockey stick takes 2.5 hours machine time and 1.5 hours of craftsman time. In a day the factory is available up to 80 hours of machine time and 70 hours of craftsman time. Show that in order to make maximum profit the factory should produce only cricket bats given that the profit on a cricket bat and hockey sticks are Rs50 and Rs35 respectively.

Answer 1

Hint: We have to maximize the profit . We can solve this question by linear programming .Total machine time for making both bat and hockey stick should be less than 70. Similarly total craftsman time for making both bat and hockey stick should be less than 80. We can write these statements in equation form. Then we have to maximize the maximum function in the range. In order to do that we can test the function at corner points only.

Complete step-by-step solution:
Let’s take the number of cricket bats produced in a day is x and number of hockey sticks is y.
So according to the question –
Total machine time for making both bat and hockey stick should be less than 70 .
That means $2x+1.5y\le 70$
Total craftsman time for making both bat and hockey stick should be less than 80.
That gives us $1.5x+2.5y\le 80$
Production of bat and hockey stick can’t be less than 0. Converting this statements to equation we get $x\ge 0$ and $y\ge 0$
We have to maximize the profit that means we have to maximize $50x+35y$

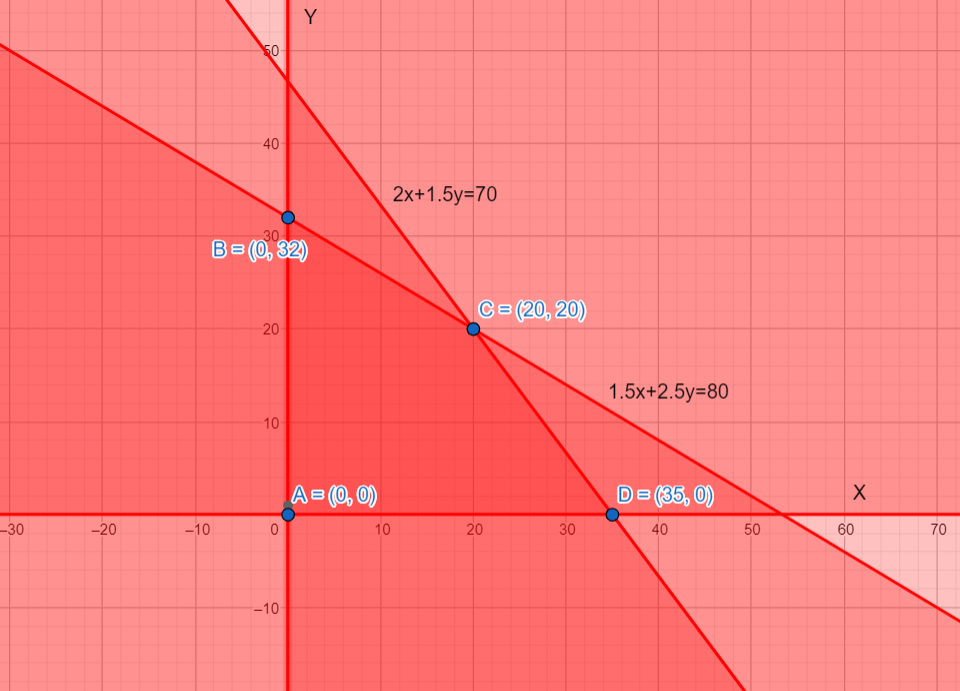
The darker red region is our range.
The corner points are A $\left( 0,0 \right)$ , B $\left( 0,32 \right)$, C$\left( 35,0 \right)$ and D $\left( 20,20 \right)$
Our maximize equation $50x+35y$
At A $\left( 0,0 \right)$ the profit will be 0.
At B $\left( 0,32 \right)$ the profit will be $0\times 50+32\times 35=1120$
At C $\left( 20,20 \right)$ the profit will be $20\times 50+20\times 35=1700$
At D $\left( 35,0 \right)$ the profit will be $35\times 50+0\times 35=1750$
So the maximum will be at $\left( 35,0 \right)$ . That means production of bats is 35 and hockey sticks is 0.

Note: In these types of questions we have to find the maximize or minimize equation for the function which we have to maximize or minimize in a specific region. To get the region we can note down the inequalities the question has to follow. Then we can find the corner point at which we can test the function and find the point at which function will be maximum. Sometimes the region will be infinite, in that case we have to check whether there exists a maximum value or it will be infinity.