
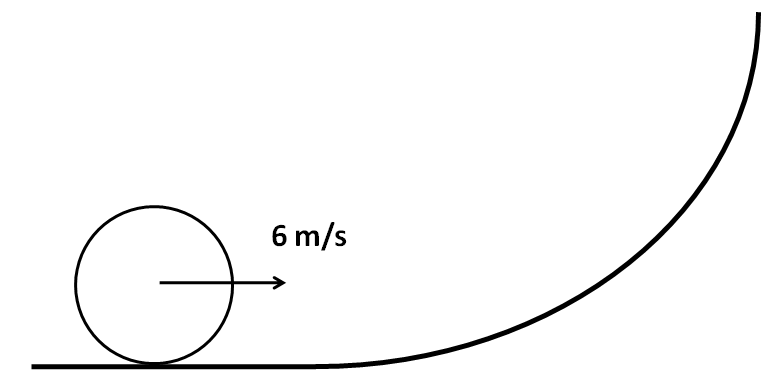
A disc of radius $0.1m$ rolls without sliding on a horizontal surface with a velocity of $6m{s^{ - 1}}$. Then, it ascends a smooth continuous track as shown in the figure. Given, $g = 10m{s^{ - 2}}$, the height up to which it will ascend is $\left( {g = 10m{s^{ - 2}}} \right)$
(A) $2.4m$
(B) $0.9m$
(C) $2.7m$
(D) $1.8m$

Answer
554.1k+ views
Hint To solve this question, we need to use the principle of conservation of energy. Since the track is smooth, no frictional force will act on the disc. The only force which will act is the conservative gravitational force, so that the total mechanical energy of the disc will be conserved. So we need to find the total kinetic energy of the disc, which will be the sum of the translational and the kinetic energy of the disc. Then this energy has to be equated with the potential energy at the highest point to get the final value of the height.
Formula used: The formulae used to solve this question are
${K_T} = \dfrac{1}{2}m{v^2}$
${K_R} = \dfrac{1}{2}I{\omega ^2}$
$v = \omega R$
$U = mgh$
$I = \dfrac{1}{2}m{R^2}$
Complete step-by-step solution:
Let $m$ be the mass of the disc.
Since the disc is rolling as well as translating forward, its kinetic energy will be the sum of the translational and the rotational components. So the kinetic energy is given by
$K = {K_T} + {K_R}$
$ \Rightarrow K = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}I{\omega ^2}$ ………………….(1)
It is given that the disc is rolling without sliding. Therefore, we have
$v = \omega R$
$ \Rightarrow \omega = \dfrac{v}{R}$ ……………………..(2)
Also, we know that the moment of inertia of a disc is given by
$I = \dfrac{1}{2}m{R^2}$..........................(3)
Substituting (2) and (3) in (1) we get
$K = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}\left( {\dfrac{1}{2}m{R^2}} \right){\left( {\dfrac{v}{R}} \right)^2}$
$ \Rightarrow K = \dfrac{1}{2}m{v^2} + \dfrac{1}{4}m{R^2}\left( {\dfrac{{{v^2}}}{{{R^2}}}} \right)$
On simplifying, we get
$K = \dfrac{1}{2}m{v^2} + \dfrac{1}{4}m{v^2}$
$ \Rightarrow K = \dfrac{3}{4}m{v^2}$ ……………………….(4)
Let us take the potential energy at the horizontal level equal to zero. So the total energy of the disc at the horizontal level is equal to the kinetic energy, that is,
${E_1} = K$
$ \Rightarrow {E_1} = \dfrac{3}{4}m{v^2}$............................(5)
Now, let $h$ be the maximum height ascended by the disc. So the potential energy of the disc at the highest point is given by
$U = mgh$
The kinetic energy of the disc at the highest point will be equal to zero. So total mechanical energy of the disc at the highest point is equal to the potential energy, that is,
${E_2} = U$
$ \Rightarrow {E_2} = mgh$.............................(6)
Since no non-conservative force act on the disc, its mechanical energy is conserved, that is,
${E_1} = {E_2}$
Putting (5) and (6) we get
$\dfrac{3}{4}m{v^2} = mgh$
Cancelling $m$ from both sides
$\dfrac{3}{4}{v^2} = gh$
$ \Rightarrow h = \dfrac{{3{v^2}}}{{4g}}$
According to the question, $v = 6m{s^{ - 1}}$ and $g = 10m{s^{ - 2}}$. Putting these above, we finally get
$h = \dfrac{{3{{\left( 6 \right)}^2}}}{{40}}$
$ \Rightarrow h = 2.7m$
Hence, the correct answer is option C.
Note: Do not forget to calculate the rotational kinetic energy of the disc along with the translational kinetic energy. This is done since the disc is not only translating, but also rotating. We can also attempt this question using the work energy theorem. For that, we have to calculate the work done by the gravitational force, and equate it with the change in the kinetic energy of the disc to get the same equation as obtained in the above solution.
Formula used: The formulae used to solve this question are
${K_T} = \dfrac{1}{2}m{v^2}$
${K_R} = \dfrac{1}{2}I{\omega ^2}$
$v = \omega R$
$U = mgh$
$I = \dfrac{1}{2}m{R^2}$
Complete step-by-step solution:
Let $m$ be the mass of the disc.
Since the disc is rolling as well as translating forward, its kinetic energy will be the sum of the translational and the rotational components. So the kinetic energy is given by
$K = {K_T} + {K_R}$
$ \Rightarrow K = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}I{\omega ^2}$ ………………….(1)
It is given that the disc is rolling without sliding. Therefore, we have
$v = \omega R$
$ \Rightarrow \omega = \dfrac{v}{R}$ ……………………..(2)
Also, we know that the moment of inertia of a disc is given by
$I = \dfrac{1}{2}m{R^2}$..........................(3)
Substituting (2) and (3) in (1) we get
$K = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}\left( {\dfrac{1}{2}m{R^2}} \right){\left( {\dfrac{v}{R}} \right)^2}$
$ \Rightarrow K = \dfrac{1}{2}m{v^2} + \dfrac{1}{4}m{R^2}\left( {\dfrac{{{v^2}}}{{{R^2}}}} \right)$
On simplifying, we get
$K = \dfrac{1}{2}m{v^2} + \dfrac{1}{4}m{v^2}$
$ \Rightarrow K = \dfrac{3}{4}m{v^2}$ ……………………….(4)
Let us take the potential energy at the horizontal level equal to zero. So the total energy of the disc at the horizontal level is equal to the kinetic energy, that is,
${E_1} = K$
$ \Rightarrow {E_1} = \dfrac{3}{4}m{v^2}$............................(5)
Now, let $h$ be the maximum height ascended by the disc. So the potential energy of the disc at the highest point is given by
$U = mgh$
The kinetic energy of the disc at the highest point will be equal to zero. So total mechanical energy of the disc at the highest point is equal to the potential energy, that is,
${E_2} = U$
$ \Rightarrow {E_2} = mgh$.............................(6)
Since no non-conservative force act on the disc, its mechanical energy is conserved, that is,
${E_1} = {E_2}$
Putting (5) and (6) we get
$\dfrac{3}{4}m{v^2} = mgh$
Cancelling $m$ from both sides
$\dfrac{3}{4}{v^2} = gh$
$ \Rightarrow h = \dfrac{{3{v^2}}}{{4g}}$
According to the question, $v = 6m{s^{ - 1}}$ and $g = 10m{s^{ - 2}}$. Putting these above, we finally get
$h = \dfrac{{3{{\left( 6 \right)}^2}}}{{40}}$
$ \Rightarrow h = 2.7m$
Hence, the correct answer is option C.
Note: Do not forget to calculate the rotational kinetic energy of the disc along with the translational kinetic energy. This is done since the disc is not only translating, but also rotating. We can also attempt this question using the work energy theorem. For that, we have to calculate the work done by the gravitational force, and equate it with the change in the kinetic energy of the disc to get the same equation as obtained in the above solution.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




