Question

A disc of mass \[10g\] is found floating horizontally by throwing $10$ marbles per second against it from below. The marbles strike the disc normally and rebound downwards with an equal speed. If the mass of each marble is\[5g\], the velocity with which the marbles are striking the disc is \[\left( g=9.8m{{s}^{-2}} \right)\]
\[\begin{align}
  & A.0.98m{{s}^{-2}} \\
 & B.9.8m{{s}^{-2}} \\
 & C.1.96m{{s}^{-2}} \\
 & D.19.6m{{s}^{-2}} \\
\end{align}\]

Answer 1

Hint: When the marbles get rebounded back, the velocity change will be the twice of the velocity of each marble. Thus the momentum also will be double the value of individual momentum. When we calculate the total momentum per sec, the individual momentum is being multiplied by the number of marbles striking per sec. These all will help you in solving this question.

Complete step by step answer:

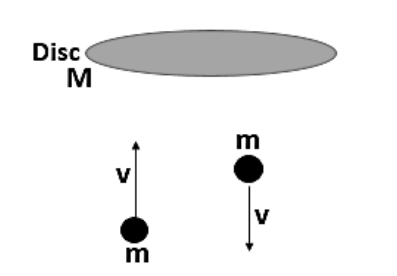
As per mentioned in the question
The mass of the disc is given as,
\[M=10g=0.01kg\]
Mass of the marble striking the disc will be,
\[m=5g=0.005kg\]
Let us take that the number of marbles striking per sec be\[n\], and the velocity with which the marbles are striking the disc be\[v\].
Therefore the weight of the disc acting downward is given as,
\[w=Mg\]
The change in velocity occurring due to the rebounding of the marbles can be written as,
\[\Delta v=v-\left( -v \right)=2v\]
This is because the marbles are rebounding back therefore their velocity will be negative.
Hence the change in the momentum is given as,
\[\Delta P=m\times 2v\]
This is the case of individual marble. The change in momentum of n marbles per second can be written when this value of momentum change is multiplied with the number of marbles incident per second.
Therefore total momentum change occurring per sec can be written as,
\[\Delta p=2mnv\]
This will be equal to the force exerted by the marbles in the upward direction.
The disc will be at rest itself as the net force acting on it is zero and also it is at rest initially too.
Therefore for the disc to be remain at rest,
Weight of the disc will be equal to the upward force on it.
\[Mg=2mnv\]
Rearranging this equation will give the velocity with which the marbles are striking,
\[v=\dfrac{Mg}{2mn}\]
Where the number of marbles incident per second is given as,
$n=10$
Substituting the values in the equation,
\[\begin{align}
  & v=\dfrac{Mg}{2mn}=\dfrac{\left( 0.01\times 9.8 \right)}{\left( 2\times 0.005\times 10 \right)} \\
 & v=0.98m{{s}^{-1}} \\
\end{align}\]
Therefore the correct answer is option A.

Note: Momentum refers to the quantity of motion that a body is having. There are two types of momentum. Linear momentum and angular momentum. A body which is spinning has angular momentum and a mass moving with a velocity is having linear momentum.