
A dietician wishes to mix two types of foods in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 10 units of vitamin C. Food I contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C while Food II contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C. It costs Rs.5 per kg to purchase Food I and Rs.7 per kg to purchase Food II. Determine the minimum cost of such a mixture. Formulate the above as an LPP and solve it graphically.
Answer
580.5k+ views
Hints: To solve this question through LPP, at first we must represent the constraints in respective inequations by assuming the amount of food I and food Ii in the mixture as two different variables. Then we will consider the inequations as the equation of the straight line and draw them in the graph. We require any two points to draw the straight line which is obtained by substituting arbitrary abscissa values in the equation of the straight line and solving to get the corresponding ordinate value. Then we must trace the common feasible region in accordance with the inequations. Finally, by determining the minimum coordinate of the point of the feasible region in the graph we will get the minimum cost.
Let’s consider the mixture contains x Kg of food I and y Kg of food II.
Complete step-by-step solution:
From the question, it is given that the vitamin contents of the mixture contain at least 8 units vitamin A and 10 units vitamin C. The total vitamin A content in mixture is\[2x + y\]. Similarly total vitamin C content in the mixture is\[x + 2y\]. According to the question the inequations are given by
\[2x + y \geqslant 8\] …………………………………………. (1)
\[x + 2y \geqslant 10\] …………………………………………. (2)
\[x \geqslant 0\] …………………………………………. (3)
\[y \geqslant 0\] …………………………………………. (4)
Let z be the total cost of purchasing x kg of food I and y kg of food II. Given cost of food I is 5 rupees/kg and cost of food II is 7 rupees per kg.
Now
\[z = 5x + 7y\] …………………………………………. (5)
Here we have to minimize z subject to the inequations (1), (2), (3), and (4). Let’s draw the lines of inequation (1) and (2) and trace the feasible region.
For inequation (1)
We must draw the line of inequation (1) passing through \[(0,8)\]and\[(1,6)\].
For inequation (2)
We must draw the line of inequation (2) passing through \[(0,5)\]and \[(2,4)\]
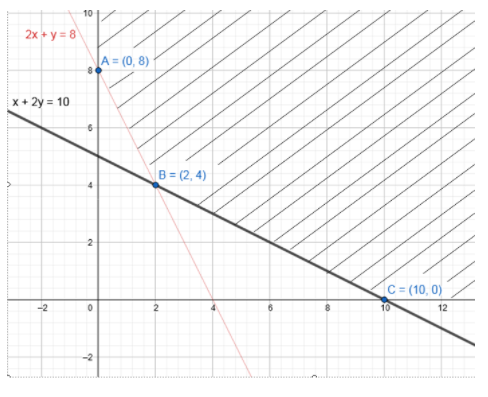
The shaded region is the feasible region.
Now from the graph, the corner points obtained in the feasible region A\[(0,8)\], B\[(2,4)\]and
C\[(10,0)\] must be considered to get the minimum value of z.
For point A\[(0,8)\]
\[z = 5 \times 0 + 7 \times 8 = 56\]
For point B\[(2,4)\]
\[z = 5 \times 2 + 7 \times 4 = 38\]
For point C\[(10,0)\]
\[z = 5 \times 10 + 7 \times 0 = 50\]
From the 3 points we get the minimum value of z is 38 corresponding to point \[(2,4)\] as the abscissa and ordinates here are 2 and 4 respectively.
Thus the minimum cost of the mixture is 38 Rupees per kg.
Note: While tracing the feasible region it should be noted that the region should be common corresponding to all of the constraints. The feasible region for a general inequation \[Ax + By \geqslant C\]must be the region representing the continuous region from the boundary of the straight line in the positive direction of x and y and the feasible region for a general inequation \[Ax + By \leqslant C\]must be the region representing the continuous region from the boundary of the straight line in the negative direction of x and y.
Let’s consider the mixture contains x Kg of food I and y Kg of food II.
Complete step-by-step solution:
From the question, it is given that the vitamin contents of the mixture contain at least 8 units vitamin A and 10 units vitamin C. The total vitamin A content in mixture is\[2x + y\]. Similarly total vitamin C content in the mixture is\[x + 2y\]. According to the question the inequations are given by
\[2x + y \geqslant 8\] …………………………………………. (1)
\[x + 2y \geqslant 10\] …………………………………………. (2)
\[x \geqslant 0\] …………………………………………. (3)
\[y \geqslant 0\] …………………………………………. (4)
Let z be the total cost of purchasing x kg of food I and y kg of food II. Given cost of food I is 5 rupees/kg and cost of food II is 7 rupees per kg.
Now
\[z = 5x + 7y\] …………………………………………. (5)
Here we have to minimize z subject to the inequations (1), (2), (3), and (4). Let’s draw the lines of inequation (1) and (2) and trace the feasible region.
For inequation (1)
| x | 0 | 1 |
| \[y = 8 - 2x\] | 8 | 6 |
We must draw the line of inequation (1) passing through \[(0,8)\]and\[(1,6)\].
For inequation (2)
| x | 0 | 2 |
| \[y = \dfrac{{10 - x}}{2}\] | 5 | 4 |
We must draw the line of inequation (2) passing through \[(0,5)\]and \[(2,4)\]

The shaded region is the feasible region.
Now from the graph, the corner points obtained in the feasible region A\[(0,8)\], B\[(2,4)\]and
C\[(10,0)\] must be considered to get the minimum value of z.
For point A\[(0,8)\]
\[z = 5 \times 0 + 7 \times 8 = 56\]
For point B\[(2,4)\]
\[z = 5 \times 2 + 7 \times 4 = 38\]
For point C\[(10,0)\]
\[z = 5 \times 10 + 7 \times 0 = 50\]
From the 3 points we get the minimum value of z is 38 corresponding to point \[(2,4)\] as the abscissa and ordinates here are 2 and 4 respectively.
Thus the minimum cost of the mixture is 38 Rupees per kg.
Note: While tracing the feasible region it should be noted that the region should be common corresponding to all of the constraints. The feasible region for a general inequation \[Ax + By \geqslant C\]must be the region representing the continuous region from the boundary of the straight line in the positive direction of x and y and the feasible region for a general inequation \[Ax + By \leqslant C\]must be the region representing the continuous region from the boundary of the straight line in the negative direction of x and y.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Two Planoconcave lenses 1 and 2 of glass of refractive class 12 physics CBSE

The compound 2 methyl 2 butene on reaction with NaIO4 class 12 chemistry CBSE

Bacterial cell wall is made up of A Cellulose B Hemicellulose class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Give 10 examples of unisexual and bisexual flowers




