
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin content of one kg of food is given below:
Food Vitamin A Vitamin B Vitamin C X 1 2 3 Y 2 2 1
One kg of food X cost Rs.16 and one kg of food Y costs Rs.20. find the least cost of the mixture which will produce the required diet?
| Food | Vitamin A | Vitamin B | Vitamin C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
Answer
558.6k+ views
Hint: We solve this by the method of linear inequality. We know that ‘at least’ means that ‘greater than or equal to’, we use this to make an inequality. From the given table we obtain three inequality. We get one inequality from costs of the food, we minimize this inequality to get the least cost of the mixture.
Complete step-by-step answer:
Let, the mixture contains x units of food X.
The mixture contains y units of the food Y.
From the given data,
\[ \bullet \] Vitamin A content in one kg of food:
Food X contains \[ \to 1 \times x\] units
Food Y contains \[ \to 2 \times y\] units
Total requirement is \[ \to \] at least 10
\[\therefore x + 2y \geqslant 10\] . ----- (1)
\[ \bullet \] Vitamin B content in one kg of food
Food X contains \[ \to 2 \times x\] units
Food Y contains \[ \to 2 \times y\] units
Total requirement is \[ \to \] at least 12
\[\therefore 2x + 2y \geqslant 12\] (Divide by 2)
\[\therefore x + y \geqslant 6\] ------- (2)
\[ \bullet \] Vitamin C content in one kg of food
Food X contains \[ \to 3 \times x\] units
Food Y contains \[ \to 1 \times y\] units
Total requirement is \[ \to \] at least 8
\[\therefore 3x + y \geqslant 8\] ----- (3).
Also we have, \[x \geqslant 0\] and \[y \geqslant 0\] .
As, we need to find the minimize cost of the mixture, we use the function: Minimize Z
Now food X cost \[ \to \] Rs. 16
Food Y cost \[ \to \] Rs. 20.
\[\therefore Z = 16x + 20y\] . -------- (4)
Combining all constraints:
Min \[Z = 16x + 20y\] subject to the constraints,
\[x + 2y \geqslant 10\] , \[x + y \geqslant 6\] , \[3x + y \geqslant 8\] , \[x \geqslant 0\] and \[y \geqslant 0\] .
Now, we have
\[x + 2y \geqslant 10\]
\[x + y \geqslant 6\]
\[3x + y \geqslant 8\]
We find the above values by putting \[x = 0\] , we find the value of \[y\] and putting \[y = 0\] we find the value of \[x\] .
Let’s see for the first inequality,
\[x = 0\] in inequality (1).
\[ \Rightarrow 0 + 2y = 10\]
\[ \Rightarrow y = \dfrac{{10}}{2}\]
\[ \Rightarrow y = 5\]
Now put \[y = 0\]
\[ \Rightarrow x + 2 \times 0 = 10\]
\[ \Rightarrow x = 10\] .
Similarly we can find for the other two inequality and listed in the above tabular column.
Now let’s draw the graph,
Scale: X-axis=1 unit =2 units
Y-axis=1 unit = 2 units.
Since all the inequalities are ‘greater than equal to’ it is obvious that we shade the above the line.
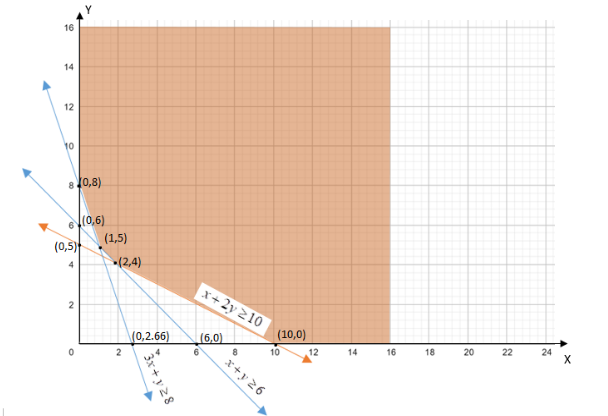
Now from the graph we have,
We obtained the value of Z by substituting x and y value in the inequality (4).
Lets see for corner points (2, 4)
\[Z = 16x + 20y\] , put \[x = 2\] and \[y = 4\]
\[ \Rightarrow Z = (16 \times 2) + (20 \times 4)\]
\[ \Rightarrow Z = 32 + 80\]
\[ \Rightarrow Z = 112\] . Similarly we can find other corner points and are listed in the above tabular column.
We can see the feasible region is unbounded.
Hence 112 may or may not be the minimum value of Z.
For this we need to draw graph inequality:
\[16x + 20y < 112\] (Divide by 4)
\[4x + 5Y < 28\] .
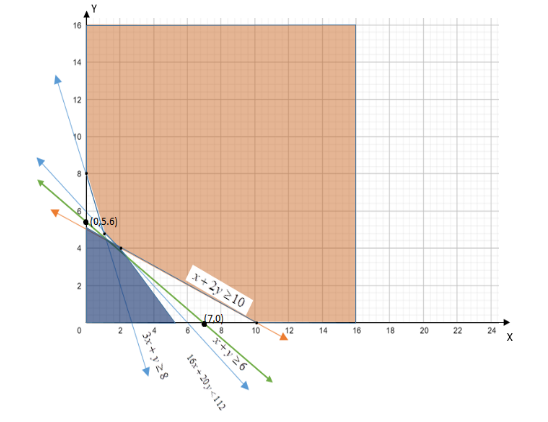
Since, there is no point in common Between the Feasible region and inequality.
Hence, the minimum value of Z is 112.
We have a minimum value at the corner points (2, 4).
Hence the cost of mixture will be minimum if 2 packets of food X and 4 packets of Food Y are used. Minimum cost is Rs. 112
So, the correct answer is “112”.
Note: If we see in the above graph we did not shade on the negative X-axis and negative Y-axis. This is because \[x \geqslant 0\] and \[y \geqslant 0\] . Feasible means shaded region. We converted the given word problem into inequalities and then we solved it. Careful while drawing a graph, as we can see above the problem depends on the graph we drawn.
Complete step-by-step answer:
Let, the mixture contains x units of food X.
The mixture contains y units of the food Y.
From the given data,
\[ \bullet \] Vitamin A content in one kg of food:
Food X contains \[ \to 1 \times x\] units
Food Y contains \[ \to 2 \times y\] units
Total requirement is \[ \to \] at least 10
\[\therefore x + 2y \geqslant 10\] . ----- (1)
\[ \bullet \] Vitamin B content in one kg of food
Food X contains \[ \to 2 \times x\] units
Food Y contains \[ \to 2 \times y\] units
Total requirement is \[ \to \] at least 12
\[\therefore 2x + 2y \geqslant 12\] (Divide by 2)
\[\therefore x + y \geqslant 6\] ------- (2)
\[ \bullet \] Vitamin C content in one kg of food
Food X contains \[ \to 3 \times x\] units
Food Y contains \[ \to 1 \times y\] units
Total requirement is \[ \to \] at least 8
\[\therefore 3x + y \geqslant 8\] ----- (3).
Also we have, \[x \geqslant 0\] and \[y \geqslant 0\] .
As, we need to find the minimize cost of the mixture, we use the function: Minimize Z
Now food X cost \[ \to \] Rs. 16
Food Y cost \[ \to \] Rs. 20.
\[\therefore Z = 16x + 20y\] . -------- (4)
Combining all constraints:
Min \[Z = 16x + 20y\] subject to the constraints,
\[x + 2y \geqslant 10\] , \[x + y \geqslant 6\] , \[3x + y \geqslant 8\] , \[x \geqslant 0\] and \[y \geqslant 0\] .
Now, we have
\[x + 2y \geqslant 10\]
| x | 0 | 10 |
| y | 5 | 0 |
\[x + y \geqslant 6\]
| x | 0 | 6 |
| y | 6 | 0 |
\[3x + y \geqslant 8\]
| x | 0 | 2.66 |
| y | 8 | 0 |
We find the above values by putting \[x = 0\] , we find the value of \[y\] and putting \[y = 0\] we find the value of \[x\] .
Let’s see for the first inequality,
\[x = 0\] in inequality (1).
\[ \Rightarrow 0 + 2y = 10\]
\[ \Rightarrow y = \dfrac{{10}}{2}\]
\[ \Rightarrow y = 5\]
Now put \[y = 0\]
\[ \Rightarrow x + 2 \times 0 = 10\]
\[ \Rightarrow x = 10\] .
Similarly we can find for the other two inequality and listed in the above tabular column.
Now let’s draw the graph,
Scale: X-axis=1 unit =2 units
Y-axis=1 unit = 2 units.
Since all the inequalities are ‘greater than equal to’ it is obvious that we shade the above the line.

Now from the graph we have,
| Corner Points | Value of Z |
| (0, 8) | 160 |
| (1, 5) | 116 |
| (2, 4) | 112 |
| (10, 0) | 120 |
We obtained the value of Z by substituting x and y value in the inequality (4).
Lets see for corner points (2, 4)
\[Z = 16x + 20y\] , put \[x = 2\] and \[y = 4\]
\[ \Rightarrow Z = (16 \times 2) + (20 \times 4)\]
\[ \Rightarrow Z = 32 + 80\]
\[ \Rightarrow Z = 112\] . Similarly we can find other corner points and are listed in the above tabular column.
We can see the feasible region is unbounded.
Hence 112 may or may not be the minimum value of Z.
For this we need to draw graph inequality:
\[16x + 20y < 112\] (Divide by 4)
\[4x + 5Y < 28\] .
| x | 7 | 0 |
| y | 0 | 5.6 |

Since, there is no point in common Between the Feasible region and inequality.
Hence, the minimum value of Z is 112.
We have a minimum value at the corner points (2, 4).
Hence the cost of mixture will be minimum if 2 packets of food X and 4 packets of Food Y are used. Minimum cost is Rs. 112
So, the correct answer is “112”.
Note: If we see in the above graph we did not shade on the negative X-axis and negative Y-axis. This is because \[x \geqslant 0\] and \[y \geqslant 0\] . Feasible means shaded region. We converted the given word problem into inequalities and then we solved it. Careful while drawing a graph, as we can see above the problem depends on the graph we drawn.
Recently Updated Pages
Questions & Answers - Ask your doubts

A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Two Planoconcave lenses 1 and 2 of glass of refractive class 12 physics CBSE

The compound 2 methyl 2 butene on reaction with NaIO4 class 12 chemistry CBSE

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

What is pollution? How many types of pollution? Define it





