
A cylindrical rod of length h is melted and cast into a cone of base radius twice that of cylinder. What is the height of the cone?
(a)$\dfrac{3h}{4}$
(b)$\dfrac{4h}{4}$
(c)2h
(d)$\dfrac{h}{2}$
Answer
595.2k+ views
Hint: We will use the formula of volume of cylinder $\pi {{r}^{2}}h$ and volume of cone $\dfrac{\pi {{r}^{2}}h}{3}$ and then we will equate them and then substitute the given values and use the relation between the radius and substitute it in the formula to find the height of cone in terms of height of cylinder h.
Complete step-by-step answer:
Let’s look at the figures,
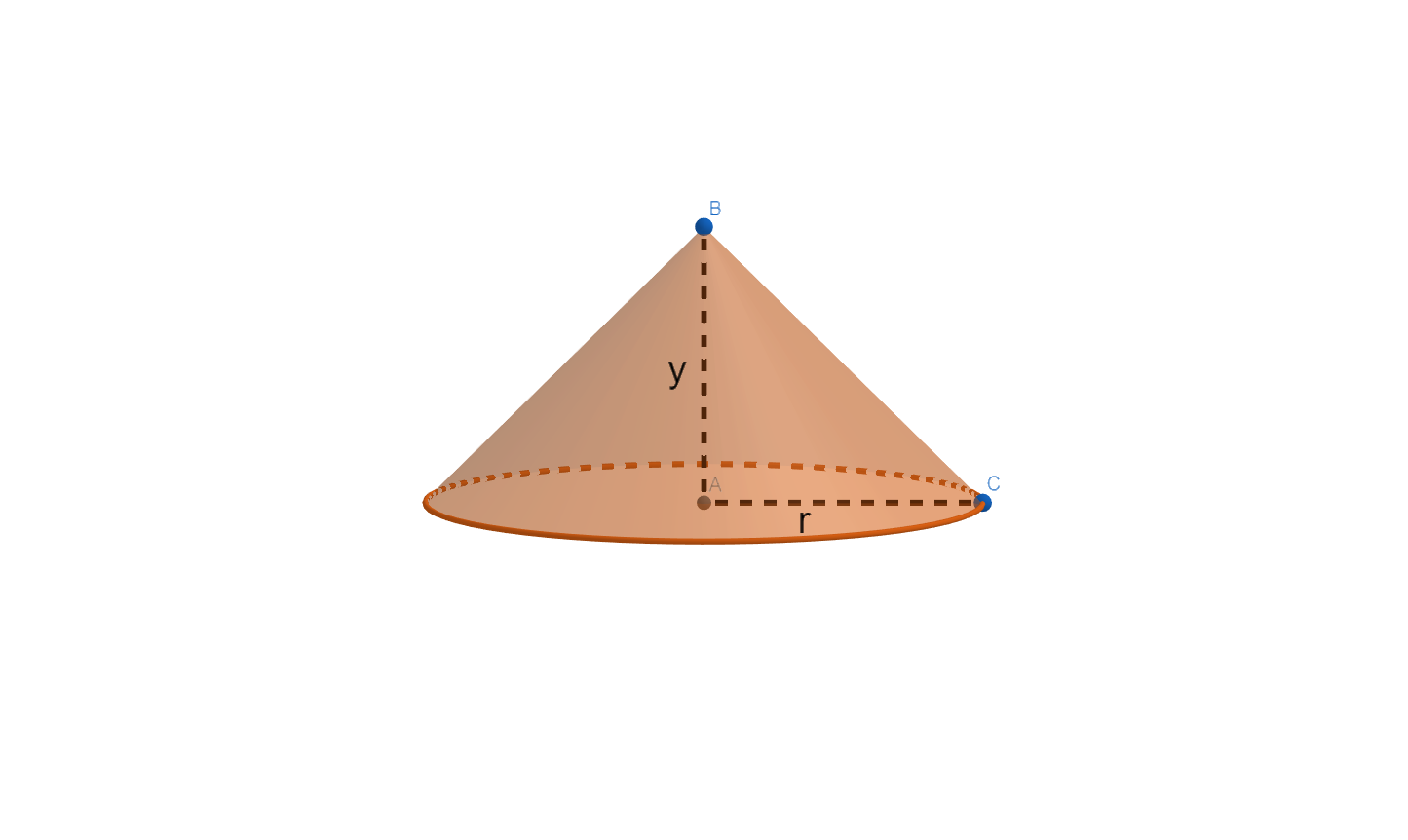
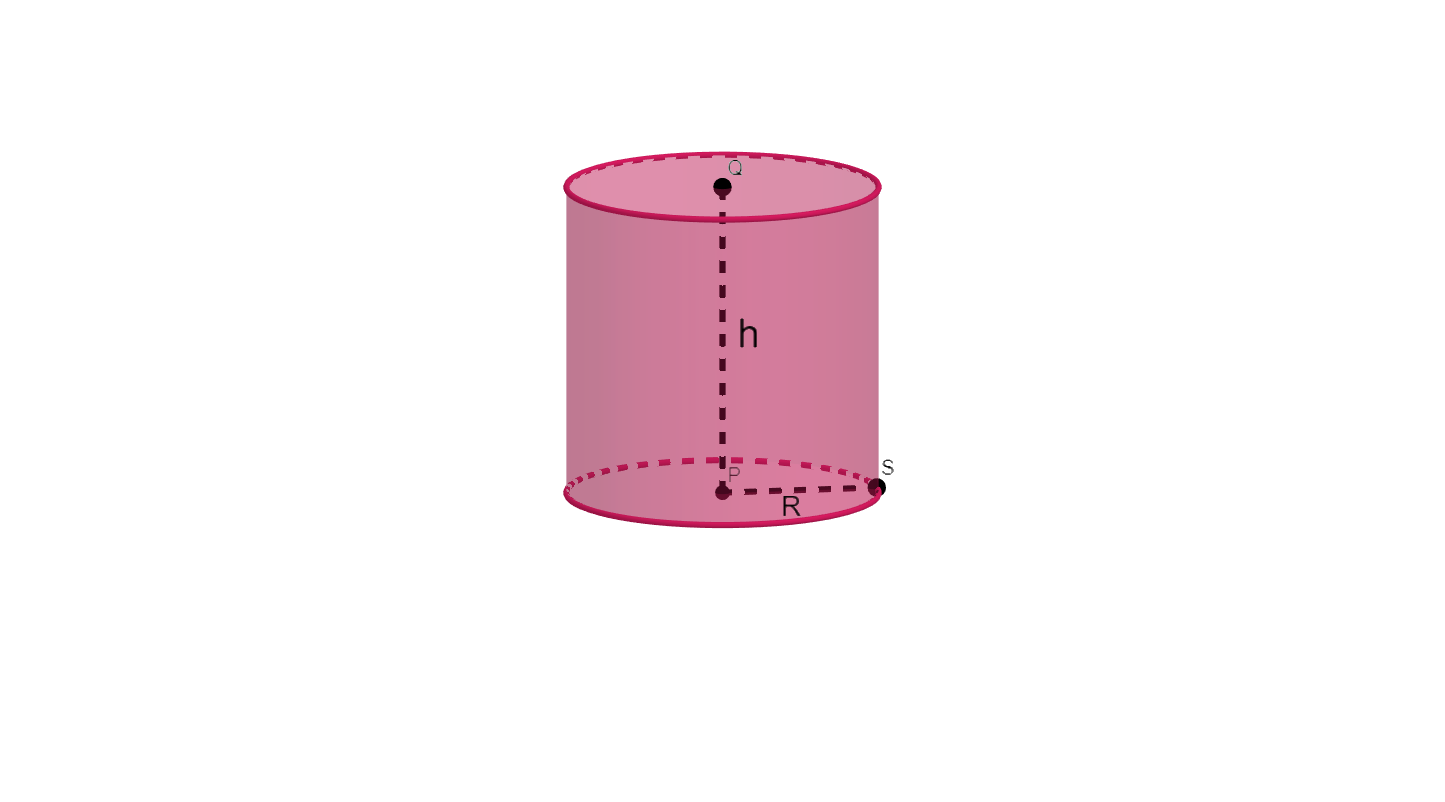
The formula for volume of cylinder is $\pi {{r}^{2}}h$ and volume of cone is $\dfrac{\pi {{r}^{2}}h}{3}$
Let the height of the cone be y and radius be r.
Hence, the volume of the cone will be $\dfrac{\pi {{r}^{2}}y}{3}...........(1)$
Now let the radius of the cylinder be R and the height is given as h.
Hence, the volume of cylinder will be $\pi {{R}^{2}}h.............(2)$
Now it is given in the question that the radius of the cone is twice that of the cylinder.
Hence, r = 2R.
Now using this relation in (1) we get,
Volume of cone as $\dfrac{\pi {{\left( 2R \right)}^{2}}y}{3}$
Now the same cylindrical is melted into a cone, therefore their volume must be the same.
Hence we get,
$\begin{align}
& \dfrac{\pi {{\left( 2R \right)}^{2}}y}{3}=\pi {{R}^{2}}h \\
& 4{{R}^{2}}y=3{{R}^{2}}h \\
& y=\dfrac{3h}{4} \\
\end{align}$
Hence, the height of cone is $\dfrac{3h}{4}$
Hence, option (a) is correct.
Note: The formula of volume of cone $\dfrac{\pi {{r}^{2}}h}{3}$ and the volume of cylinder $\pi {{r}^{2}}h$ must be kept in mind, and one should know how to use the given information in the question to find the height of cone. Given that the cylinder is melted and formed to a cone, one should be able to understand that their volume will be the same in this case. Also, in the question, we have to find the height of the cone and options are in terms of ‘h’, so we must not take the height of the cone as ‘h’ but some other variable to avoid confusions while calculation.
Complete step-by-step answer:
Let’s look at the figures,


The formula for volume of cylinder is $\pi {{r}^{2}}h$ and volume of cone is $\dfrac{\pi {{r}^{2}}h}{3}$
Let the height of the cone be y and radius be r.
Hence, the volume of the cone will be $\dfrac{\pi {{r}^{2}}y}{3}...........(1)$
Now let the radius of the cylinder be R and the height is given as h.
Hence, the volume of cylinder will be $\pi {{R}^{2}}h.............(2)$
Now it is given in the question that the radius of the cone is twice that of the cylinder.
Hence, r = 2R.
Now using this relation in (1) we get,
Volume of cone as $\dfrac{\pi {{\left( 2R \right)}^{2}}y}{3}$
Now the same cylindrical is melted into a cone, therefore their volume must be the same.
Hence we get,
$\begin{align}
& \dfrac{\pi {{\left( 2R \right)}^{2}}y}{3}=\pi {{R}^{2}}h \\
& 4{{R}^{2}}y=3{{R}^{2}}h \\
& y=\dfrac{3h}{4} \\
\end{align}$
Hence, the height of cone is $\dfrac{3h}{4}$
Hence, option (a) is correct.
Note: The formula of volume of cone $\dfrac{\pi {{r}^{2}}h}{3}$ and the volume of cylinder $\pi {{r}^{2}}h$ must be kept in mind, and one should know how to use the given information in the question to find the height of cone. Given that the cylinder is melted and formed to a cone, one should be able to understand that their volume will be the same in this case. Also, in the question, we have to find the height of the cone and options are in terms of ‘h’, so we must not take the height of the cone as ‘h’ but some other variable to avoid confusions while calculation.
Recently Updated Pages
Questions & Answers - Ask your doubts

A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Two Planoconcave lenses 1 and 2 of glass of refractive class 12 physics CBSE

The compound 2 methyl 2 butene on reaction with NaIO4 class 12 chemistry CBSE

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

What is pollution? How many types of pollution? Define it





