Question

A current time curve is shown in the following diagram. This type of current is passed in the primary coil of the transformer. The nature of induced emf in the secondary coil will be

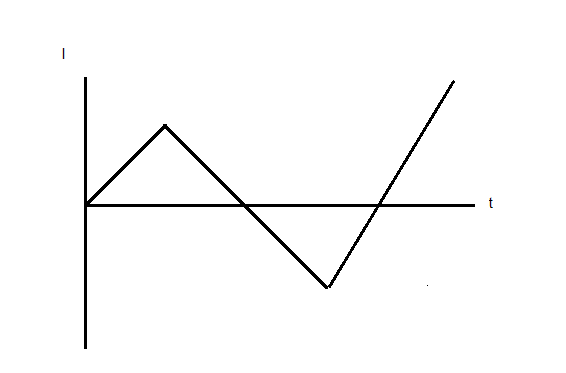
Answer 1

Hint: current can be alternating or direct. An AC is that current which changes its direction after every half cycle while on the other hand direct current does not. Transformer works on the principle of mutual induction. Current in the primary coil produces a magnetic flux in the secondary coil which continuously keeps on changing as a result of magnetic induction current being induced in it.

Complete step by step answer:
From Faraday’s law of electromagnetic induction, emf induced in the secondary coil is given by the expression, \[e=\dfrac{d\varphi }{dt}\], where \[\varphi \]is the magnetic flux in the second coil.
Flux by gauss law is given as \[\varphi \]= BA where B is the magnetic field and A is the area of the coil. Thus,
\[e=A\dfrac{dB}{dt}\]
But, \[\dfrac{dB}{dt}\alpha \dfrac{dI}{dt}\]
\[\Rightarrow e\alpha \dfrac{dI}{dt}\]
So, we need to just differentiate the current with respect to time. Doing this with our given graph, we find a constant line parallel to the time axis. so, graph for emf will be lines parallel to time axis

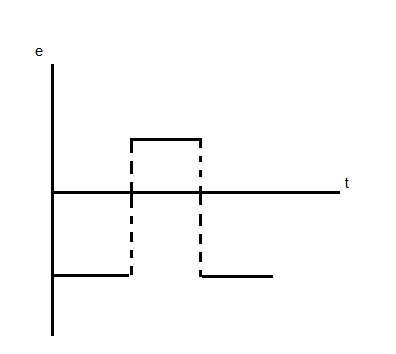
Note:
There are certain laws which we need to keep in our mind while using differentiation. For a constant quantity, differentiation always yields zero. Also, if the quantity is increasing then its differentiation will yield a positive number while for the opposite case it will yield a negative number. Transformer involves flux loss too but that can be minimized.