Question

A current ${{I}_{1}}$ caring wire AB is placed near another long CD carrying current ${{I}_{2}}$. If wire AB is free to move, it will have:

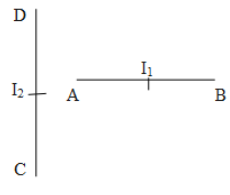
A. rotational motion only
B. translational motion only
C. rotational as well as translational motion
D. neither rotational nor translational motion.

Answer 1

Hint: When a current is flowing through a conductor a magnetic force is developed around the conductor. When an external free moving charge or current carrying conductor will come into contact with this magnetic field the conductor will experience a certain amount of force. Due to this force, the free body will undergo some sort of motion.

Complete answer:
Ina straight current carrying conductor a magnetic field is developed around the conductor which is assumed to be in a circular path around the conductor.

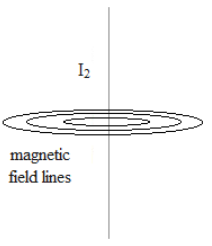
The magnetic field developed around the conductor is by Biot-savart's law.
According to Biot-savart's law, the magnetic field is given
\[d\vec{B}={{\mu }_{0}}\dfrac{Idl\sin \theta }{4\pi {{r}^{2}}}\]

So as derived from Biot-savart's law the magnetic field around the conductor CD is,
\[d\vec{B}={{\mu }_{0}}\dfrac{{{I}_{2}}}{2\pi r}\]
The intensity of this magnetic field decreases as we move away from the conductor. So the magnitude of the magnetic field decreases along the wire AB due to wire CD.
On each element (small element) of wire AB, the force experienced will be equal to ${{I}_{1}}Bdr$
As a result of which the wire AB will perform both translational and rotational motions. The translation motion will be due to the reason that all forces acting in upward direction and rotation will be due to all forces being different in magnitudes.

So the correct option is option C.

Note:
When there is a change in the electric or magnetic field along a conductor some amount of emf is induced in the conductor. This emf is termed as induced emf. This emf opposes the changes occurring and due to that induced is in the opposite direction of the force-producing it.