Question

A cuboid water tank is 6m long, 5m wide and 4.5m deep. How many liters of water can it hold?

Answer 1

Hint: In this question, we are given the measurement of a cuboid water tank and need to find the volume of water it can hold. For this, we need to find the volume of the cuboid water tank using the formula of the volume of the cuboid given by $V=l\times b\times h$ where V is the volume of the cuboid, l is the length of the cuboid, b is the breadth of the cuboid and h is the height of the cuboid. Since we will get volume in ${{m}^{3}}$ but we want volume in liters, so, we will use the following formula for conversion $1{{m}^{3}}=1000l$.

Complete step-by-step answer:
Given cuboidal water tank will look like this,

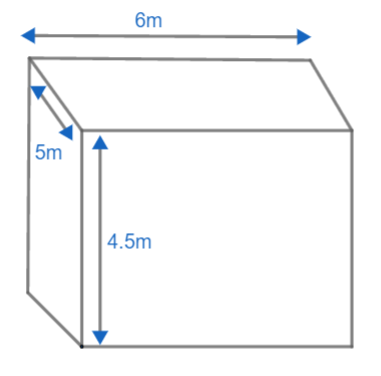
Here, the length is 6m, therefore l = 6m.
The breadth is 5m, therefore b = 5m.
The height is 4.5m, therefore h = 4.5m.
As we know, the volume of a cuboid is given by $V=l\times b\times h$ where, V is the volume of the cuboid, l is the length of the cuboid, b is the breadth of the cuboid and h is the height of the cuboid.
Hence, volume of the given cuboid water tank will be given by,
\[\begin{align}
  & V=l\times b\times h \\
 & \Rightarrow V=6m\times 4.5m\times 5m \\
 & \Rightarrow V=135{{m}^{3}} \\
\end{align}\]
Hence, the volume of the cuboidal water tank is $135{{m}^{3}}$. So it can hold 135 cubic meters of water. But we need to find the volume of water it can hold in liters. So let us convert the units of volume using the following formula: 1 cubic meter = 1000 liters.
Hence, $135{{m}^{3}}=\left( 1000\times 135 \right)\text{Liters}=135000\text{Liters}$.
Hence, the given cuboidal water tank can hold 135000 liters of water.

Note: Students should always take care of the units while solving these sums. They should check that all the given measurements must be in the same units. Here depth and height are the same , width and breadth are the same. If we were given measurements in cm, then in liters $1000c{{m}^{3}}=1\text{Liters}$.