Question

A cubical block of wood of edge a and density \[\rho \] floats in water of density \[2\rho \]. The lower surface of the cube just touches the free end of a massless spring of force constant k, fixed at the bottom of the vessel. The weight W put over the block so that it completely immersed in the water without wetting the weight is

(A) \[a\left( {{a^2}\rho g + K} \right)\]
(B) \[a\left( {a\rho g + 2K} \right)\]
(C) \[a\left( {\dfrac{{a\rho g}}{2} + 2K} \right)\]
(D) \[a\left( {{a^2}\rho g + \dfrac{K}{2}} \right)\]

Answer 1

Hint:Determine the length of edge of the block immersed in the water before placing the weight over it. Then balance the forces acting on the block to determine the weight of the block.

Formula used:
\[\Rightarrow{F_b} = {\rho _l}{V_o}g\]
Here, \[{\rho _l}\] is the density of the liquid, \[{V_o}\] is the volume of the object immersed in the liquid and g is the acceleration due to gravity.

Complete step by step answer:
Initially the block is just touching the free end of a massless spring, that means there is no compression in the spring due to zero net force. We have to determine how much the edge of the block is immersed in the water before the weight is placed over it.
Initially, two forces acting on the block are the buoyant force due to water and the weight of the block. Since the block is stationary at a certain distance, the buoyant force and the weight of the block balance each other. Therefore, we can write,
\[\Rightarrow{F_b} = W\]
\[ \Rightarrow {\rho _w}{V_b}g = {m_b}g\] ……(1)
Here, \[{\rho _w}\] is the density of water, \[{V_b}\] is the block of the water immersed in the water, \[{m_b}\] is the mass of the block and g is the acceleration due to gravity.
Volume of the wooden block is, \[{V_b} = {a^2}x\]. Here, x is the portion of the block immersed in the water.
The mass of the block is the density of the block multiplied by the volume of the block. Therefore,
\[\Rightarrow{m_b} = {a^3}\rho \]
Therefore, equation (1) becomes,
\[\Rightarrow \left( {2\rho } \right)\left( {{a^2}x} \right) = {a^3}\rho \]
Thus, half of the block is immersed in the water.
When the weight is placed over the wooden block, it is completely immersed in the water and the compression in the spring is \[\dfrac{a}{2}\].
The spring force is equal to the force constant multiplied by the compression in the spring.
\[\Rightarrow{F_s} = kx\]
Draw the free body diagram of the forces acting on the wooden block as shown in the figure below.

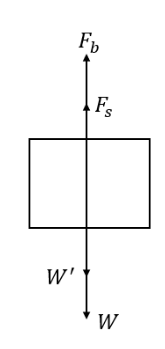
In the above diagram, \[W'\] is the buoyant force, \[{F_s}\] is the spring force, \[W'\] is the weight that is placed over a wooden block and W is the weight of the wooden block.
From the above diagram, we can write,
\[\Rightarrow {F_b} + {F_s} = W + W'\]
\[ \Rightarrow \left( {2\rho } \right)\left( {{a^3}} \right)g + K\dfrac{a}{2} = \left( {{a^3}\rho g} \right) + W'\]
\[\Rightarrow W' = \left( {2\rho } \right)\left( {{a^3}} \right)g + K\dfrac{a}{2} - {a^3}\rho g\]
\[
\Rightarrow W' = {a^3}\rho g + \dfrac{{Ka}}{2} \\
\Rightarrow\therefore W' = a\left( {{a^2}\rho g + \dfrac{K}{2}} \right) \\
\]

So, the correct answer is option (D).

Note:Since the spring compresses downwards doesn’t mean the force of compression is in the downward direction. The spring force is in the opposite direction of the compression of the spring.