
A copper disc of radius 0.1m rotated about its center with 10 revolutions per second in a uniform magnetic field of 0.1 tesla with its plane perpendicular to the field. The e.m.f induced across the radius of disc is:
$
A.{\text{ }}\dfrac{\pi }{{10}}volt \\
B.{\text{ }}\dfrac{{2\pi }}{{10}}volt \\
C.{\text{ }}\pi \times {\text{1}}{{\text{0}}^{ - 2}}volt \\
D.{\text{ 2}}\pi \times {10^{ - 2}}volt
$
Answer
509.1k+ views
Hint: E.m.f induced in case of a rotating circular disk is given as $ \in = \dfrac{{B\omega {r^2}}}{2}$, where B is the magnetic field, $\omega $ is the angular frequency and r is the radius of the disc.
Formula used:
E.m.f is given as
$ \in = \dfrac{{B\omega {r^2}}}{2}$, where $\omega = 2\pi \upsilon $
Complete answer:
In this question, we have a copper disc (a good conductor of electricity) having radius 0.1m. It is rotating with a frequency of 10 revolutions per second and is placed in a magnetic field of 0.1T perpendicular to the plane of disc. Therefore we have the following parameters available with us.
$r = 0.1m \\
\upsilon = 10{\sec ^{ - 1}} \\
B = 0.1T \\
$
The formula for calculating the induced e.m.f is given as
$ \in = \dfrac{{0.1T \times 2\pi \times 10{{\sec }^{ - 1}} \times {{(0.1m)}^2}}}{2} $
Solving this equation, we get
$ \in = \pi \times {10^{ - 2}}volt.$
So, the correct answer is “Option C”.
Additional Information:
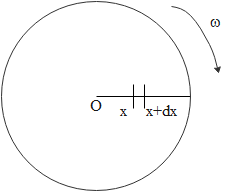
The formula used to calculate e.m.f can be derived as follows: Consider a small radial segment dx on the circular disc and the distance of this segment from the centre of the disc is x. Since the disc is moving with angular velocity $\omega $, the velocity of disc is given as $\omega x$. Therefore, we can calculate e.m.f across this segment as follows:
$d \in = vBdx = \omega xBdx$
Integrating both sides, we get
$\int {d \in = \omega B\int {xdx} } \\
\Rightarrow \in = B\omega \dfrac{{{x^2}}}{2} $
This is how we obtain the formula for e.m.f. It is simple to remember and can help in understanding the concept better.
Note:
1. All units should be in the same system of units.
2. We notice that flux is not exactly changing for this rotating disc so e.m.f should be zero according to Faraday’s law. But that is not the case, this is where Lorentz force comes into action. It acts on the charge carriers moving inside the disc.
Formula used:
E.m.f is given as
$ \in = \dfrac{{B\omega {r^2}}}{2}$, where $\omega = 2\pi \upsilon $
Complete answer:
In this question, we have a copper disc (a good conductor of electricity) having radius 0.1m. It is rotating with a frequency of 10 revolutions per second and is placed in a magnetic field of 0.1T perpendicular to the plane of disc. Therefore we have the following parameters available with us.
$r = 0.1m \\
\upsilon = 10{\sec ^{ - 1}} \\
B = 0.1T \\
$
The formula for calculating the induced e.m.f is given as
$ \in = \dfrac{{0.1T \times 2\pi \times 10{{\sec }^{ - 1}} \times {{(0.1m)}^2}}}{2} $
Solving this equation, we get
$ \in = \pi \times {10^{ - 2}}volt.$
So, the correct answer is “Option C”.
Additional Information:
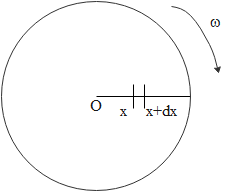
The formula used to calculate e.m.f can be derived as follows: Consider a small radial segment dx on the circular disc and the distance of this segment from the centre of the disc is x. Since the disc is moving with angular velocity $\omega $, the velocity of disc is given as $\omega x$. Therefore, we can calculate e.m.f across this segment as follows:
$d \in = vBdx = \omega xBdx$
Integrating both sides, we get
$\int {d \in = \omega B\int {xdx} } \\
\Rightarrow \in = B\omega \dfrac{{{x^2}}}{2} $
This is how we obtain the formula for e.m.f. It is simple to remember and can help in understanding the concept better.
Note:
1. All units should be in the same system of units.
2. We notice that flux is not exactly changing for this rotating disc so e.m.f should be zero according to Faraday’s law. But that is not the case, this is where Lorentz force comes into action. It acts on the charge carriers moving inside the disc.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Two Planoconcave lenses 1 and 2 of glass of refractive class 12 physics CBSE

The compound 2 methyl 2 butene on reaction with NaIO4 class 12 chemistry CBSE

Bacterial cell wall is made up of A Cellulose B Hemicellulose class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Give 10 examples of unisexual and bisexual flowers




