Question

A cooperative society of farmers has 50 hectares of land to grow two crops A and B. The profits from A and B per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. To control weeds, a liquid herbicide has to be used for crops A and B at the rate of 20 liters and 10 liters per hectare, respectively. Further not more than 800 liters of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. Keeping in mind that the protection of fish and other wildlife is more important than earning profit, how much land should be allocated to each crop so as to maximize the total profit? Form an LPP from the above and solve it graphically. Do you agree with the message that the protection of wildlife is utmost necessary to preserve the balance in the environment?

Answer 1

Hint: We first assume that ‘x’ and ‘y’ hectares are allotted to grow crops A and B. Now, we find our first constraint by using the fact that the maximum sum of x and y is 50. We now find our second constraint using the information that the maximum amount of herbicide sprayed is 800 liters. We now find the objective by using the information about the profit. We plot a graph using these constraints and find the optimal solutions from all corner point feasible solutions.

Complete step by step answer:
We have a cooperative society of farmers with 50 hectares of land to grow crops A and B.
Let us assume that the land allocated to grow crop ‘A’ be ‘x’ hectares and land allocated to grow crop ‘B’ be ‘y’ hectares.
Since, the maximum land that can be allocated is 50 hectares. We have maximum sum of ‘x’ and ‘y’ is 50.
We got our first constraint as:
$x+y\le 50$ ---(1).
To control pests, each hectare of crop A is sprayed with 20 liters of herbicide and each hectare of crop ‘B’ is sprayed with 10 liters of herbicide.
So, we have a total of 20x+10y liters of herbicide sprayed. According to the problem, we can see that the maximum amount of herbicide can be sprayed is 800 liters to conserve wild life.
So, we get maximum value of 20x+10y is 800.
We got our second constraint as:
$20x+10y\le 800$ ---(2).
According to the problem, we are getting profits of Rs 10,500 and Rs 9,000 per hectare from crops A and B. But we already allotted ‘x’ hectares to crop A and ‘y’ hectares to crop B.
We need to find total profit can be earned from all 50 hectares of land i.e., we need to find the maximum value of $10500x+9000y$.
We have got our objective function as:
Maximize $z=10500x+9000y$ ---(3).
From equations (1), (2) and (3), we combine all to get the Linear Programming Problem (LPP).
The LPP is:
Maximize $z=10500x+9000y$.
Subject to,
$x+y\le 50$.
$20x+10y\le 800$.
$x\ge 0,y\ge 0$.
Let us find the points that the given constraints touch both axes and at the point where they both intersect.
Let us find the point at which the line $x+y=50$ meet the y-axis.
We know that when the line $x+y=50$ meets y-axis, the value of x becomes zero. So, we substitute 0 in place of ‘x’ in the line $x+y=50$.
So, $0+y=50$.
$\Rightarrow y=50$.
So, the line $x+y=50$ meets y-axis at $A\left( 0,50 \right)$.
Let us find the point at which the line $20x+10y=800$ meet the x-axis.
We know that when the line $20x+10y=800$ meets x-axis, the value of y becomes zero. So, we substitute 0 in place of ‘y’ in the line $20x+10y=800$.
So, $20x+10\left( 0 \right)=800$.
$\Rightarrow 20x=800$.
$\Rightarrow x=\dfrac{800}{20}$.
$\Rightarrow x=40$.
So, the line $20x+10y=800$ meets x-axis at $C\left( 40,0 \right)$.
Let us now find the intersection point of the lines $x+y=50$ and $20x+10y=800$.
From the equation of the line $x+y=50$, we get $y=50-x$ ---(4). We substitute this in the line $20x+10y=800$.
We get $20x+10\left( 50-x \right)=800$.
$\Rightarrow 20x+500-10x=800$.
$\Rightarrow 10x=800-500$.
$\Rightarrow 10x=300$.
$\Rightarrow x=\dfrac{300}{10}$.
$\Rightarrow x=30$.
We substitute the value of x in equation (4).
$\Rightarrow y=50-30$.
$\Rightarrow y=20$.
The lines $x+y=50$ and $20x+10y=800$ intersect at $B\left( 30,20 \right)$.
We draw all the constraints in a graph to find the feasible and optimal solutions.

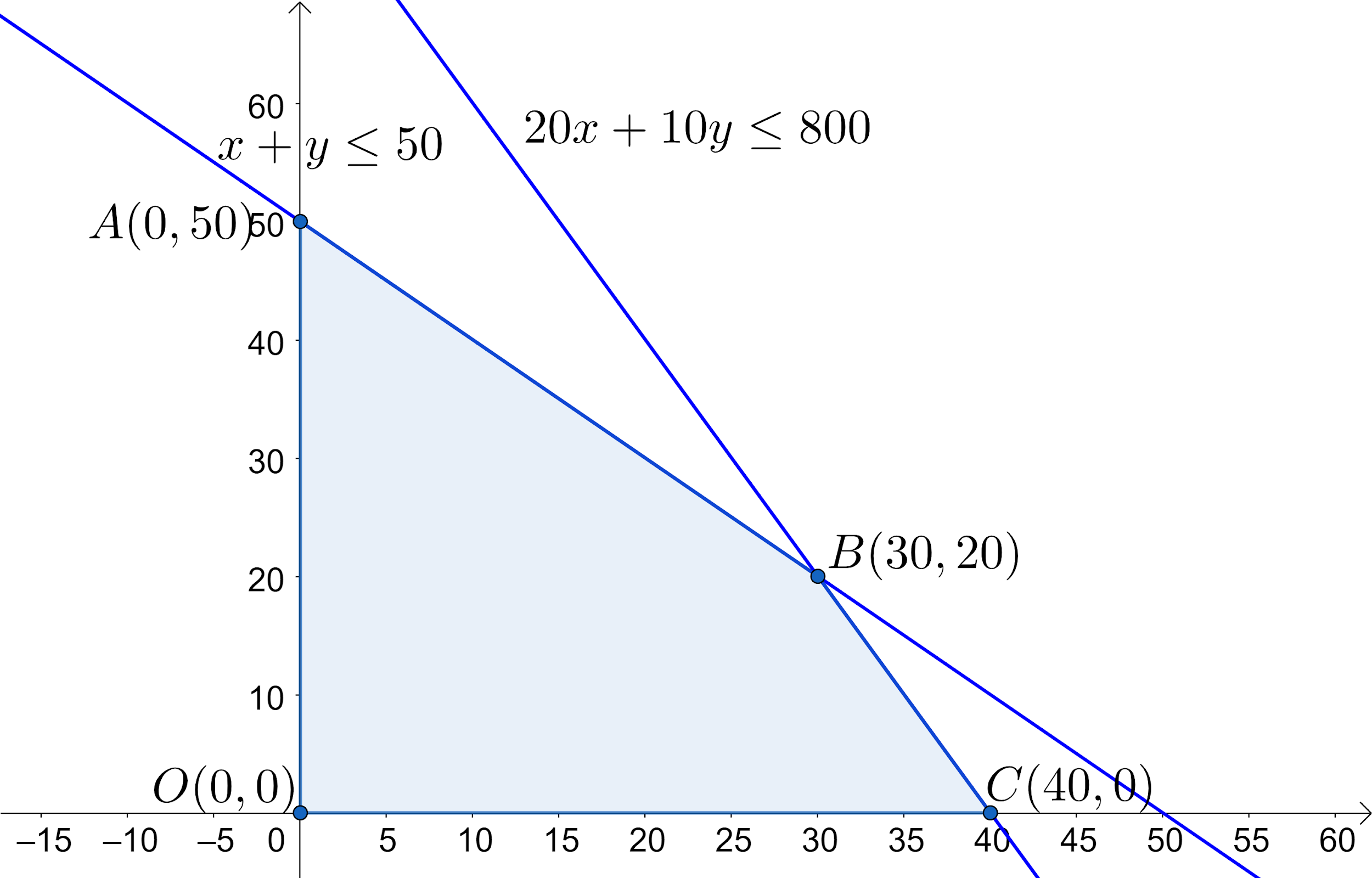
From graph, we can see that the region occupied by polygon OABC satisfies the given constraints. This region is known as feasible region.
Feasible points are every point present in the system. We have points at the corner of this feasible region. These points are known as corner point feasible solutions. We get optimal solutions from one of these corner-point feasible solutions. Let us find the value of z at each corner point of feasible solution.
At point $O\left( 0,0 \right)$, $z=10,500\left( 0 \right)+9000\left( 0 \right)=0$.
At point $A\left( 0,50 \right)$, $z=10,500\left( 0 \right)+9000\left( 50 \right)$.
At point $A\left( 0,50 \right)$, $z=450000$.
At point $B\left( 30,20 \right)$, $z=10,500\left( 30 \right)+9000\left( 20 \right)$.
At point $B\left( 30,20 \right)$, $z=315000+180000$.
At point $B\left( 30,20 \right)$, $z=495000$.
At point $C\left( 40,0 \right)$, $z=10,500\left( 40 \right)+9000\left( 0 \right)$.
At point $C\left( 40,0 \right)$, $z=420000$.
We can see that we got the maximum value of ‘z’ at $B\left( 30,20 \right)$ with a value of 495000 from all the corner point feasible solutions.

So, We allocate 30 hectares to grow crop ‘A’ and 20 hectares to grow crop ‘B’.
Yes, protection of wildlife is very important.

Note: We take $x\ge 0$ and $y\ge 0$ as the value of allotted land and herbicide sprayed cannot be negative in any case. We check corner points irrespective of the coordinates obtained. We take the answer in fractions if it is obtained in fractions unless it is mentioned as ‘x’ and ‘y’ are integers in the problem.