Question

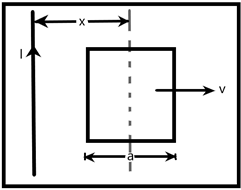
A conducting square frame of side ‘a’ and a long straight wire carrying current I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity ‘v’. The emf induced in the frame will be proportional to –
      

\[\begin{align}
& \text{A) }\dfrac{1}{{{(2x-a)}^{2}}} \\
& \text{B) }\dfrac{1}{{{(2x+a)}^{2}}} \\
& \text{C) }\dfrac{1}{(2x-a)(2x+a)} \\
& \text{D) }\dfrac{1}{{{x}^{2}}} \\
\end{align}\]

Answer 1

Hint: We need to understand the relation between the magnetic field, current flowing through a straight conducting wire and a square loop which are kept at a distance and have a relative velocity with respect to each other to solve this problem easily.

Complete answer:
We know that a moving conductor in a magnetic field can have an induced emf in it. This is from Faraday's law electromagnetic induction. We also know that a motional emf can be generated in a conductor which is moving with a certain velocity in a magnetic field.
The motional electromotive force is given as –
\[\varepsilon =Blv \]
Where, B is the magnetic field at a point, l is the length of the length of the portion of conductor under consideration and v is the velocity at which the loop is moving.
In our case, a straight current carrying conductor is the source of magnetic field. We know according to the Biot-Savart’s law the magnetic field due to a wire is proportional to the current in the wire and the distance between the wire and the loop.

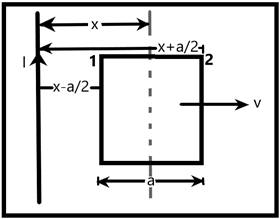
In our case, the magnetic field keeps changing as the loop is moving with a velocity. The distances at two points of motion of the loop can be as –
\[\begin{align}
& {{r}_{1}}=x-\dfrac{a}{2} \\
& {{r}_{2}}=x+\dfrac{a}{2} \\
\end{align}\]
We can use this to find the induced emf as –
\[\begin{align}
& \varepsilon =Blv \\
& \Rightarrow \varepsilon =({{B}_{2}}-{{B}_{1}})lv \\
& \Rightarrow \varepsilon =\left( \dfrac{{{\mu }_{0}}I}{2\pi {{r}_{1}}}-\dfrac{{{\mu }_{0}}I}{2\pi {{r}_{2}}} \right)lv \\
& \Rightarrow \varepsilon =\dfrac{{{\mu }_{0}}Ilv}{2\pi }\left( \dfrac{1}{x-\dfrac{a}{2}}-\dfrac{1}{x+\dfrac{a}{2}} \right) \\
& \Rightarrow \varepsilon =\dfrac{{{\mu }_{0}}Ilv2}{2\pi }\left( \dfrac{1}{2x-a}-\dfrac{1}{2x+a} \right) \\
& \Rightarrow \varepsilon =\dfrac{{{\mu }_{0}}Ilv}{\pi }\left( \dfrac{2x+a-(2x-a)}{(2x-a)(2x+a)} \right) \\
& \therefore \varepsilon \propto \dfrac{1}{(2x-a)(2x+a)} \\
\end{align}\]
The required proportionality is given above.

The correct answer is option C.

Note:
The magnetic field due to a current carrying element is dependent on the angle between the straight line joining the point and the element, but here we are considering two parallel components, so it is not required to be considered to solve.