Question

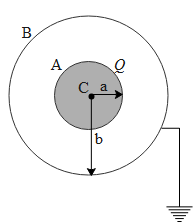
A conducting sphere A of radius a, with charge Q, is placed concentrically inside a conducting shell B of radius b. B is earthed. C is the common centre of A and B. Study the following statements.
i)The potential at a distance r from C, where $a\le r\le b,\text{is }\dfrac{1}{4\pi {{\in }_{\circ }}}\left( \dfrac{Q}{r} \right)$
ii) The potential difference between A and B is $\text{ }\dfrac{1}{4\pi {{\in }_{\circ }}}\left( \dfrac{1}{a}-\dfrac{1}{b} \right)$
iii) The potential at a distance r from C, where $\text{ }a\le r\le b,\text{is}\dfrac{1}{4\pi {{\in }_{\circ }}}\left( \dfrac{1}{r}-\dfrac{1}{b} \right)$

a) Only (i) and (ii)
b) Only (ii) and (iii)
c) Only (i) and (iii)
d) All the above

Answer 1

Hint: There are few things to be kept in mind while solving the above problem. The potential inside the shell is the same that of the potential on its surface. The shells A and B are conducting shells i.e. they can induce each other. The shell B is grounded, hence all the charge will move to the ground. Hence using this equation we will analyze the potential at different points and accordingly verify the statements given.

Complete answer:
To begin with let us write the expression for potential due to a spherical shell.

Let us consider a spherical shell of radius R and the charge on the shell be Q. hence the potential at a point P from the centre of the shell is given by, $V=\text{ }\dfrac{1}{4\pi {{\in }_{\circ }}}\left( \dfrac{Q}{r} \right)$. Hence we can write the potential on the surface of the shell of radius R from the above equation as,
$V=\text{ }\dfrac{1}{4\pi {{\in }_{\circ }}}\left( \dfrac{Q}{R} \right)$. The shell B is grounded and hence all the positive charge on the shell will move to the ground. But the shell A consisting of positive charge will induce a negative charge i.e. –Q on the shell B. Hence the shell B will possess a net negative charge.
Now let us verify the above statements one by one. In the first statement we are asked to determine the potential at a point between the shells A and B. The potential at any point will be due to both the shells i.e. Potential due to shell A (${{V}_{A}}$) and Potential due to shell B (${{V}_{B}}$ ). Hence the potential at a point between a and b at a distance r from the centre is given by,

$\begin{align}
  & V={{V}_{A}}+{{V}_{B}} \\
 & V=\text{ }\dfrac{1}{4\pi {{\in }_{\circ }}}\left( \dfrac{Q}{r} \right)+\dfrac{1}{4\pi {{\in }_{\circ }}}\left( \dfrac{-Q}{b} \right) \\
 & V=\text{ }\dfrac{Q}{4\pi {{\in }_{\circ }}}\left( \dfrac{1}{r}-\dfrac{1}{b} \right) \\
\end{align}$

Hence we can say that the first statement is invalid. But if we consider the third statement three the result we obtained matches. Hence we can say that the third statement is valid.
In the second statement we are asked to calculate the potential difference between shell A and shell B. The difference is nothing but the difference in potentials on their shells.

The potential on shell A is contributed by both the shells as well as potential on shell B.
Potential on shell A is,
$\begin{align}
  & {{V}_{a}}={{V}_{A}}+{{V}_{B}} \\
 & {{V}_{a}}=\text{ }\dfrac{1}{4\pi {{\in }_{\circ }}}\left( \dfrac{Q}{a} \right)+\dfrac{1}{4\pi {{\in }_{\circ }}}\left( \dfrac{-Q}{b} \right) \\
 & {{V}_{a}}=\text{ }\dfrac{Q}{4\pi {{\in }_{\circ }}}\left( \dfrac{1}{a}-\dfrac{1}{b} \right) \\
\end{align}$
Similarly, the potential on shell B is,
$\begin{align}
  & {{V}_{b}}={{V}_{A}}+{{V}_{B}} \\
 & {{V}_{b}}=\text{ }\dfrac{1}{4\pi {{\in }_{\circ }}}\left( \dfrac{Q}{b} \right)+\dfrac{1}{4\pi {{\in }_{\circ }}}\left( \dfrac{-Q}{b} \right) \\
 & {{V}_{b}}=\text{ }\dfrac{Q}{4\pi {{\in }_{\circ }}}\left( \dfrac{1}{b}-\dfrac{1}{b} \right)=0 \\
\end{align}$
Hence the potential difference between the two shells is given by,
$\begin{align}
  & V={{V}_{a}}-{{V}_{b}} \\
 & V=\text{ }\dfrac{Q}{4\pi {{\in }_{\circ }}}\left( \dfrac{1}{a}-\dfrac{1}{b} \right)-0 \\
 & V=\text{ }\dfrac{Q}{4\pi {{\in }_{\circ }}}\left( \dfrac{1}{a}-\dfrac{1}{b} \right) \\
\end{align}$
Therefore we can conclude that the second statement is valid.

So, the correct answer is “Option B”.

Note:
The potential at any point is basically a scalar quantity. The minus sign indicates that the potential at that point is negative. In a region of negative potential no work is to be done to move a positive charge along the region. Whereas for a negative charge work has to be done in moving the charge along the region of negative potential.