Question

A concave mirror of radius of curvature R has a circular outline of radius r. A circular disk is to be placed normal to the axis at focus so that it collects all the light that is reflected from the mirror from a beam parallel to the axis. For r << R, the area of the disc has to be at least.
A) $\dfrac{{\pi {r^6}}}{{4{R^4}}}$
B) $\dfrac{{\pi {r^4}}}{{4{R^2}}}$
C) $\dfrac{{\pi {r^5}}}{{4{R^3}}}$
D) $\dfrac{{\pi {r^4}}}{{{R^2}}}$

Answer 1

Hint: Concave mirror has an inner depressed surface that reflects the surface and acts as a convergent mirror. Here the disc in circular form is given so we use here the formula of the circle. And the beam of light is parallel to the axis that passes through the center of curvature.

Complete step by step answer:
Consider a concave mirror in which the beam of light is parallel to the axis and the radius of a circular disc is r. A ray of light can reflect or pass through at the center.

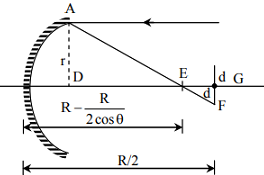
Here, d = radius of the disc
Therefore the area of circular disc (A) $ = \pi {{\text{d}}^2}$
Now, from similar triangle $\vartriangle {\text{EDA and }}\vartriangle {\text{EdF}}$ ,
$\dfrac{{\text{r}}}{{\text{d}}} = \dfrac{{{\text{R - }}\dfrac{{\text{R}}}{{2\cos \theta }}}}{{\dfrac{{\text{R}}}{2} - \left( {{\text{R - }}\dfrac{{\text{R}}}{{2\cos \theta }}} \right)}}$
$\dfrac{{\text{r}}}{{\text{d}}} = \dfrac{{2\cos \theta + 1}}{{ - \cos \theta + 1}}$
$\therefore {\text{d = }}\left( {\dfrac{{ - \cos \theta + 1}}{{2\cos \theta - 1}}} \right) \times {\text{r}}$ …………..(1)
Now, by using trigonometric ratios of right-angled triangle,
${\text{sin}}\theta {\text{ = }}\dfrac{{\text{r}}}{{\text{R}}}$
$ \Rightarrow \cos \theta = \dfrac{{\sqrt {{{\text{R}}^2} - {{\text{r}}^2}} }}{{\text{R}}}$
$\therefore cos \theta = (1-\dfrac{r^2}{R^2})^{\dfrac{1}{2}}$
$ \Rightarrow \cos \theta = 1 - \dfrac{1}{2}\dfrac{{{{\text{r}}^2}}}{{{{\text{R}}^2}}}$
Put the value of $\cos \theta $ in equation (1) where r << R
$\therefore {\text{d = }}\dfrac{{{{\text{r}}^3}}}{{{\text{2}}{{\text{R}}^2}}}$
Therefore the area of circular disc $ = \pi {{\text{d}}^2} = \pi {\left( {\dfrac{{{{\text{r}}^3}}}{{{\text{2}}{{\text{R}}^2}}}} \right)^2} = \dfrac{{\pi {{\text{r}}^6}}}{{4{{\text{R}}^4}}}$.

$\therefore$ Hence the correct option is (A).

Note:
Concave mirrors produce both real and virtual images. The image can be upright or inverted if virtual or real respectively. They can be behind the mirror if it is virtual and in front of the concave mirror, it is real. The image can be enlarged, reduced, or equal size as the object.