Question

A circular disc of radius b has a hole of radius a at its centre. If the mass per unit area of the disc varies as $(\dfrac{{{\sigma }_{0}}}{r})$, then the radius of gyration of the disc about its axis passing through the centre is:

Answer 1

Hint: For a small radius dr, we have to consider a small distribution of mass dm. We need to formulate for small change in moment of inertia and integrate it along smaller radius (a) and bigger radius (b). After obtaining a moment of inertia of the disc I, we can find the radius of gyration.

Formula used:
Radius of gyration, $k=\sqrt{\dfrac{I}{m}}$

Complete answer:
Radius of gyration of a body about an axis of rotation is defined as the radial distance to a point which would have a moment of inertia which is equal to the moment of inertia of the body’s actual distribution of mass. This is conditional to the total mass of the body being concentrated.

Let us consider the moment of inertia of the disc to be I
dI is a partial derivative of moment of inertia.

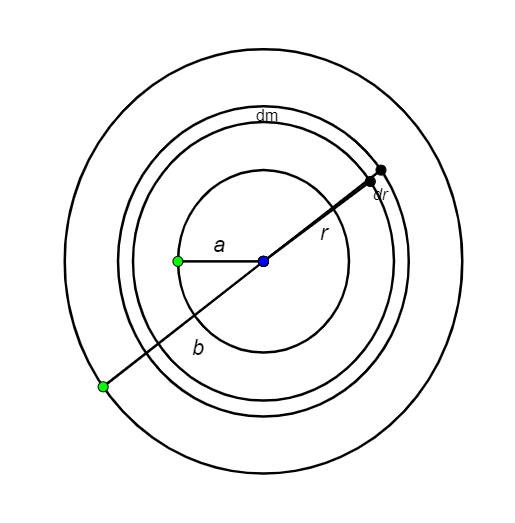
$\begin{align}
  & dI=(dm){{r}^{2}} \\
 & =(\sigma dA){{r}^{2}} \\
 & =(\dfrac{{{\sigma }_{0}}}{r}2\pi rdr){{r}^{2}} \\
 & =({{\sigma }_{0}}2\pi ){{r}^{2}}dr \\
 & I=\int{dI=\int_{a}^{b}{{{\sigma }_{0}}}}2\pi {{r}^{2}}dr \\
 & ={{\sigma }_{0}}2\pi (\dfrac{{{b}^{3}}-{{a}^{3}}}{3}) \\
 & m=\int{dm}=\int{\sigma dA} \\
 & ={{\sigma }_{0}}2\pi \int_{a}^{b}{dr} \\
 & m={{\sigma }_{0}}2\pi (b-a) \\
\end{align}$
Radius of gyration of the disc is
$\begin{align}
  & k=\sqrt{\dfrac{I}{m}}=\sqrt{\dfrac{({{b}^{3}}-{{a}^{3}})}{3(b-a)}} \\
 & =\sqrt{(\dfrac{{{a}^{2}}+{{b}^{2}}+ab}{3})} \\
\end{align}$
Hence the radius of gyration of the disc is $\sqrt{(\dfrac{{{a}^{2}}+{{b}^{2}}+ab}{3})}$

Additional Information:
The dynamics and kinematics of rotation around a fixed axis of a rigid body are algebraically much easier than those for free rotation of a rigid body. They are completely analogous to those of linear motion along a single fixed direction, which is not true for free rotation of a rigid body.

Note:
A rigid body is an object of limited reach in which all the distances between the component particles doesn’t change. Perfect rigid bodies do not exist. External forces can deform any solid. So we define a rigid body as an object that can be deformed under large forces.