Question

A child has a die whose six faces show the letters as given below:
The die is thrown once. What is the probability of getting (i) $A?$ (ii) $D?$
\[\]

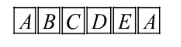
Answer 1

Hint: Use basic definition of probability:

$P\left( E \right)=\dfrac{\text{Total number favourable to cases}}{\text{Total outcomes (sample space)}}$
As we know that $P\left( E \right)=\dfrac{\text{ Number of outcomes required}}{\text{sample space (Total no}\text{. of outcomes)}}$
Here, As we can observe that we have six faces on a die with six letters, i.e., the number of total outcomes will be 6.
Let categorise the number of times letters can come by counting the number of faces at which they are present:
$\begin{align}
  & A=2 \\
 & B=1 \\
 & C=1 \\
 & D=1 \\
 & E=1 \\
\end{align}$
Hence, for any face’s letter probability
$P\left( E \right)=\dfrac{\text{Outcome of that particular letter}}{\text{Total number of outcomes }}$
(i) Probability for getting $A$
 \[\begin{align}
  & P\left( E \right)=\dfrac{\text{No}\text{. of times A can come to a face}}{\text{Total number of outcomes possible }} \\
 & P\left( E \right)=\dfrac{2}{6}=\dfrac{1}{3} \\
\end{align}\]
(ii) Probability for getting $D$
 \[\begin{align}
  & P\left( E \right)=\dfrac{\text{No}\text{. of times D can come to a face}}{\text{Total number of outcomes possible }} \\
 & P\left( E \right)=\dfrac{1}{6} \\
\end{align}\]
Note: (i) One can take the total number of outcomes as $5$ as counting the number of letters present $A,B,C,D,E$ which will be wrong because we are calculating probability with respect to the faces (once thrown written in the question).
(ii) One can think, this problem belongs to any application part of probability but here it is using the fundamental definition.