Question

A charged ball B hangs from a silk thread S which makes an angle \[\theta \] with a large charged conducting sheet P as shown in the given figure. The surface charge density \[\sigma \] of the sheet is proportional to:

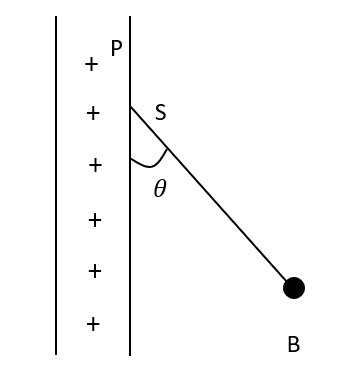
A. \[\cos \theta \]
B. \[\cot \theta \]
C. \[\sin \theta \]
D. \[\tan \theta \]

Answer 1

Hint: Draw a free body diagram indicating the forces acting on the charged ball. Equate the forces and use the relation between electric field and permittivity of the medium.

Formula used:
\[{F_e} = qE\]
Here, q is the charge of on the ball and E is the electric field.

Complete step by step answer:
The charged ball is placed in a uniform electric field experiences an electric force of magnitude,
\[{F_e} = qE\]
Here, q is the charge of on the ball and E is the electric field.Draw a free body diagram of the forces acting on the charged ball as shown in the figure below,

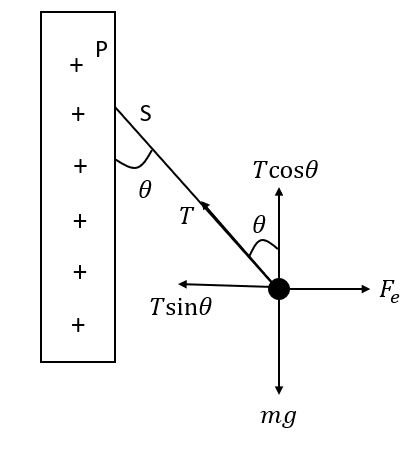
Balance the forces acting on the charged ball in the vertical direction as follows,
\[T\cos \theta = mg\] ……. (1)
Balance the forces acting on the charged ball in the horizontal direction as follows,
\[T\sin \theta = {F_e}\]
\[ \Rightarrow T\sin \theta = qE\] ……. (2)
Divide equation (2) by equation (1). \[\dfrac{{T\sin \theta }}{{T\cos \theta }} = \dfrac{{qE}}{{mg}}\]
\[ \Rightarrow \tan \theta = \left( {\dfrac{q}{{mg}}} \right)E\] ……. (3)
We know that the electric field is the ratio of surface charge density \[\sigma \]and permittivity of the medium \[\varepsilon \].
\[E = \dfrac{\sigma }{\varepsilon }\]
Substitute \[E = \dfrac{\sigma }{\varepsilon }\] in equation (3).
\[\left( {\dfrac{q}{{mg}}} \right)\dfrac{\sigma }{\varepsilon } = \tan \theta \]
\[ \Rightarrow \sigma = \left( {\dfrac{{\varepsilon mg}}{q}} \right)\tan \theta \]
\[\therefore \sigma \propto \tan \theta \]

So, the correct answer is “Option D”.

Note:
Specify the correct directions of forces acting on the charged ball whether they are along the positive direction of the y-axis or along the negative direction of the y-axis and the same for the x-axis. Here, the electric force should be along the positive direction of the x-axis.