Question

A charge moving with velocity in x-direction is subjected to a field of magnetic induction in the negative x-direction. As a result, the charge will
A) retard along X-axis
B) move along a helical path around X-axis
C) remain unaffected
D) starts moving in a circular path

Answer 1

Hint: When a moving charge is subjected to a magnetic field, the charge experiences a force. This force is proportional to the velocity of the charge as well as the strength of the magnetic field, it is subjected to. The force is also dependent on the angle between the direction of velocity of the charge and the direction of the magnetic field.

Complete answer:
When a moving charge is subjected to a magnetic field, the charge experiences a force, which is directly proportional to the velocity of the charge as well as the strength of the magnetic field, the charge is subjected to. If $\overrightarrow{V}$ is the velocity of the charge and $\overrightarrow{B}$ is the strength of magnetic field, then the force $\overrightarrow{F}$, experienced by the moving charge is proportional to the cross product of the velocity of the charge and the strength of the magnetic field. $\overrightarrow{F}$ is given by
$\overrightarrow{F}=q(\overrightarrow{V}\times \overrightarrow{B})$
where $q$ is a charge moving with a velocity $\overrightarrow{V}$ in a magnetic field of strength $\overrightarrow{B}$
Let this be equation 1.

Here, it is important to note that all the three parameters $\overrightarrow{V},\overrightarrow{B}$ and $\overrightarrow{F}$ are vectors, which have both direction as well as magnitude.
On expanding the cross product in the above expression, equation 1 can also be written as
$\overrightarrow{F}=qVB\sin \theta $
where
$V$ is the magnitude of velocity of the moving charge
$B$ is the magnitude of the magnetic field
$\theta $ is the angle between the direction of velocity of the moving charge and the direction of magnetic field
Let this be equation 2.

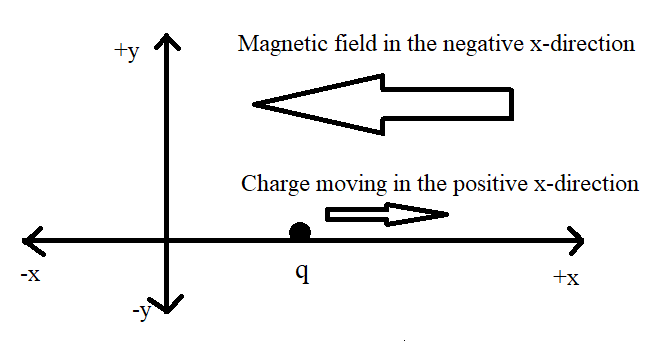
Now, let us suppose that the charge is moving with velocity in the positive x-direction as given in the question. A magnetic field due to magnetic induction is subjected to this moving charge in the negative x-direction, as shown in the figure.

It is clear from the figure that the angle between the velocity of the charge and the magnetic field is equal to $180{}^\circ $. From equation 2, the force experienced by this moving charge is given by
$\overrightarrow{F}=qVB\sin \theta =qVB\sin (180{}^\circ )=qVB(0)=0$

Therefore, it can be stated that no force is acting on this moving charge due to the magnetic field. The charge maintains the same velocity and moves on. Hence, it can be said that the charge will remain unaffected.

So, the correct answer is “Option C”.

Note:
It is to be noted that the force experienced by the moving charge in all the equations mentioned above remains in the vector form. This suggests that the force can either be positive or negative, depending upon the angle between the velocity of the charge and the direction of the magnetic field, as well as the charge itself. The direction of force is perpendicular to the plane formed by velocity and the magnetic field, and is given by the right-hand rule. If the right thumb points towards the direction of velocity of a moving charge and if the other fingers on the right-hand point towards the direction of magnetic field, then the direction of force is perpendicular to the plane formed by the right thumb and the other fingers on the right hand.