Question

A bullet of mass \[m\] moving with a velocity \[v\]strikes a block of mass \[M\]at rest and gets embedded to it. The kinetic energy of the composite block will be
 \[\begin{align}
  & A)\dfrac{1}{2}m{{v}^{2}}\times \dfrac{m}{\left( m+M \right)} \\
 & B)\dfrac{1}{2}m{{v}^{2}}\times \dfrac{M}{\left( m+M \right)} \\
 & C)\dfrac{1}{2}m{{v}^{2}}\times \dfrac{\left( m+M \right)}{M} \\
 & D)\dfrac{1}{2}m{{v}^{2}}\times \dfrac{\left( m+M \right)}{m} \\
\end{align}\]

Answer 1

Hint: We will use the law of conservation of momentum which is given as initial momentum of the system will be equal to final momentum of the system to determine the final velocity of the combined block. Then we will use the expression for kinetic energy to find the kinetic energy of the given system using the velocity we found. Kinetic energy is directly proportional to mass and square of the velocity of the body.

Formula used:
\[\begin{align}
  & {{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \\
 & K.E=\dfrac{1}{2}m{{v}^{2}} \\
\end{align}\]

Complete step by step answer:
Firstly we will draw a diagram for understanding the situation better.

                     

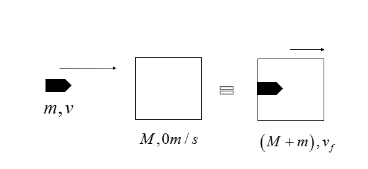
Here, the mass of the bullet is taken as \[m\].
Mass of the block is taken as \[M\].
Velocity of the bullet is taken as \[v\].
And velocity of the block is zero as it is initially at rest.
Now, we will use the law of conservation of momentum to find the velocity of the combined block whose mass will be \[M+m\]. That is,
 \[mv+M\times 0=\left( m+M \right){{v}_{f}}\]

 \[\begin{align}
  & \Rightarrow mv=\left( m+M \right){{v}_{f}} \\
 & \Rightarrow {{v}_{f}}=\dfrac{m}{\left( m+M \right)}v \\
\end{align}\]

So, the final velocity of the combined block is found to be, \[{{v}_{f}}=\dfrac{m}{\left( m+M \right)}v\].
Now, we will use this velocity to find the kinetic energy of the combined block. Kinetic energy is given as,
         \[K.E=\dfrac{1}{2}m{{v}^{2}}\]
We have the mass of the combined block as \[M+m\].
 \[\begin{align}
     & \Rightarrow K.E=\dfrac{1}{2}\left( m+M \right){{\left( \dfrac{m}{\left( m+M \right)}v \right)}^{2}} \\
 &\Rightarrow K.E=\dfrac{1}{2}\left( m+M \right)\times \dfrac{{{m}^{2}}}{{{\left( m+M \right)}^{2}}}{{v}^{2}} \\
 & \Rightarrow K.E=\dfrac{1}{2}m{{v}^{2}}\times \dfrac{m}{\left( m+M \right)} \\
\end{align}\]

Hence, we have found the kinetic energy of composite block as\[\dfrac{1}{2}m{{v}^{2}}\times \dfrac{m}{\left( m+M \right)}\].
Hence, the correct answer is option A.

Note:
We must be very careful while doing problems like this. The sign of velocity has a major role in determining the momentum. In this case the velocity of all the objects and systems is in the same direction which we have taken as positive. But we must remember that we will need to use sign convention if any of the colliding particles or the composite system has a change in direction in velocity.