-
Courses-
Crash Courses 2021
-
Olympiads/NTSE/Others
-
Micro Courses
-
Vedantu Super Kids NEW
-
Reading & Spoken English -
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
Questions & Answers
Question
Answers
Related Questions
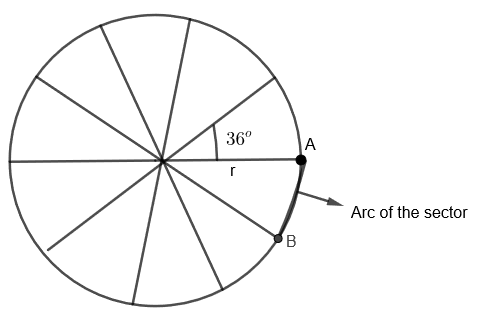
A brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in the fig. Find:
(i) The total length of the silver wire required
(ii) The arc of each sector of the brooch.
Answer
![Verified]()
Verified
Verified
Hint: First of all, draw the diagram of the brooch to get a clear idea about it. Then find the length of the wire by taking the sum of the circumference and 5 diameters. As the circumference is divided into 10 arcs, accordingly find its value.
Complete step-by-step answer:
Here, we are given that a brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The same wire is also used in making 5 diameters which divide the circle into 10 equal sectors. We have to find the length of the wire required and the arc of each sector of the brooch.
(i) We can diagrammatically show the brooch as:
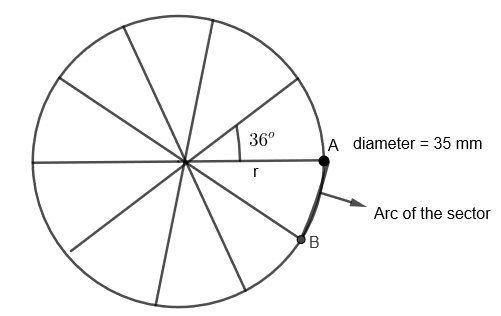
This brooch has diameter = 35 mm
We know that radius of the circle \[=\dfrac{\text{Diameter}}{2}\]
Therefore, we get the radius of this brooch \[=\dfrac{35}{2}=17.5mm\]
Here, we are given that the silver wire is used to make the circumference as well as 5 diameters of the circular brooch. Therefore, we get the total length of the silver wire used as:
Length of wire used = Circumference of Circle + Length of 5 diameters
We know that the circumference of a circle \[=2\pi r\], where r is the radius of the circle. By using this in the length of wire used, we get,
Length of wire used \[=2\pi r+5\times \left( \text{length of diameter} \right)\]
We know that diameter = 2r. Therefore, we get,
Length of wire used \[=2\pi r+5\times \left( 2r \right)\]
\[=2\pi r+10r\]
By substituting the value of r = 17.5 mm, we get,
Length of the wire used \[=2\pi \left( 17.5 \right)+10\left( 17.5 \right)\]
We know that \[\pi =\dfrac{22}{7}\]. Therefore, we get,
Length of the wire used \[=2\times \dfrac{22}{7}\times \left( 17.5 \right)+10\left( 17.5 \right)\]
So, we get the length of the wire = 110 + 175 = 285 mm.
Hence, we get the length of the wire required to make a circular brooch with 5 diameters is 285 mm.
(ii) Now we have to find the arc length of each sector.
We know that the circular brooch is divided into 10 sectors and the total angle at the center of the circle \[=2\pi \]
So, we get the angle of each sector
\[=\dfrac{2\pi }{\text{Number of Sectors}}=\dfrac{2\pi }{10}radians\]
Therefore, we get the angle of each sector at the center \[=\dfrac{\pi }{5}\text{radian}\]
Now, we know that the arc length \[=r\theta \] where \[\theta \] is the angle of the sector at the center in radians.
So, we get the arc length of the sector (AB) \[=r.\dfrac{\pi }{5}mm\]
We know that r = 17.5 mm and \[\pi =\dfrac{22}{7}\]. So we get,
Arc length (AB) = \[17.5\times \dfrac{22}{7\times 5}=11mm\]
So, we get the value of arc length of each sector = 11 mm.
Note: Here, students often make this mistake if substituting the length of diameter in place of the radius. So they must first check what is given in the question, then properly substitute it. Also, here students can directly find the length of the arc as follows,
We know that the circumference is divided into 10 arcs,
So, the length of 1 arc \[=\dfrac{\text{Circumference}}{10}\]
\[\Rightarrow \dfrac{2\pi r}{10}=\dfrac{\pi r}{5}\]
We are given that r = 17.5 mm and \[\pi =\dfrac{22}{7}\]
So, we get an arc length of each sector \[=\dfrac{22\left( 17.5 \right)}{7\times 5}=11mm\]
Complete step-by-step answer:
Here, we are given that a brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The same wire is also used in making 5 diameters which divide the circle into 10 equal sectors. We have to find the length of the wire required and the arc of each sector of the brooch.
(i) We can diagrammatically show the brooch as:
This brooch has diameter = 35 mm
We know that radius of the circle \[=\dfrac{\text{Diameter}}{2}\]
Therefore, we get the radius of this brooch \[=\dfrac{35}{2}=17.5mm\]
Here, we are given that the silver wire is used to make the circumference as well as 5 diameters of the circular brooch. Therefore, we get the total length of the silver wire used as:
Length of wire used = Circumference of Circle + Length of 5 diameters
We know that the circumference of a circle \[=2\pi r\], where r is the radius of the circle. By using this in the length of wire used, we get,
Length of wire used \[=2\pi r+5\times \left( \text{length of diameter} \right)\]
We know that diameter = 2r. Therefore, we get,
Length of wire used \[=2\pi r+5\times \left( 2r \right)\]
\[=2\pi r+10r\]
By substituting the value of r = 17.5 mm, we get,
Length of the wire used \[=2\pi \left( 17.5 \right)+10\left( 17.5 \right)\]
We know that \[\pi =\dfrac{22}{7}\]. Therefore, we get,
Length of the wire used \[=2\times \dfrac{22}{7}\times \left( 17.5 \right)+10\left( 17.5 \right)\]
So, we get the length of the wire = 110 + 175 = 285 mm.
Hence, we get the length of the wire required to make a circular brooch with 5 diameters is 285 mm.
(ii) Now we have to find the arc length of each sector.
We know that the circular brooch is divided into 10 sectors and the total angle at the center of the circle \[=2\pi \]
So, we get the angle of each sector
\[=\dfrac{2\pi }{\text{Number of Sectors}}=\dfrac{2\pi }{10}radians\]
Therefore, we get the angle of each sector at the center \[=\dfrac{\pi }{5}\text{radian}\]
Now, we know that the arc length \[=r\theta \] where \[\theta \] is the angle of the sector at the center in radians.
So, we get the arc length of the sector (AB) \[=r.\dfrac{\pi }{5}mm\]
We know that r = 17.5 mm and \[\pi =\dfrac{22}{7}\]. So we get,
Arc length (AB) = \[17.5\times \dfrac{22}{7\times 5}=11mm\]
So, we get the value of arc length of each sector = 11 mm.
Note: Here, students often make this mistake if substituting the length of diameter in place of the radius. So they must first check what is given in the question, then properly substitute it. Also, here students can directly find the length of the arc as follows,
We know that the circumference is divided into 10 arcs,
So, the length of 1 arc \[=\dfrac{\text{Circumference}}{10}\]
\[\Rightarrow \dfrac{2\pi r}{10}=\dfrac{\pi r}{5}\]
We are given that r = 17.5 mm and \[\pi =\dfrac{22}{7}\]
So, we get an arc length of each sector \[=\dfrac{22\left( 17.5 \right)}{7\times 5}=11mm\]
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
