Question

A bridge across a valley is 800 meters long. There is a temple in the valley directly below the bridge. The angle of depression of the top of the temple from the two ends of the bridge measures ${30^ \circ }$ and ${60^ \circ }$. Find the height of the bridge above the top of the temple.

Answer 1

Hint: Draw a diagram to clearly analyse the situation. Two right angled triangles will be formed for the two end points of the bridge. Calculate the height of the bridge above the top of the temple using one of the triangles and then put this value for another triangle.

Complete step-by-step answer:
                               

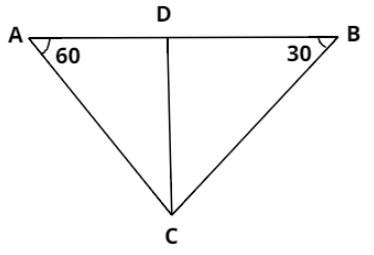
Consider the above figure. A and B are two end points of the bridge.
The length of the bridge is given in the question as 800 meters. So, we have:
$ \Rightarrow AB = 800m .....(i)$
Next, C is the position of the temple. Angles of depression on the top of the temple from the end points of the temple are given as ${30^ \circ }$ and ${60^ \circ }$. So, we get:
$ \Rightarrow \angle CBA = {30^ \circ }{\text{ and }}\angle CAB = {60^ \circ }$
We have to calculate the height of the bridge above the top of the temple. From the figure, this height is CD. So, we have to calculate the length of CD. Let its value is h.
$ \Rightarrow CD = h .....(ii)$
Now, let $AD = x .....(iii)$
As we can see from the figure, $AD + DB = AB$
And from equation $(i)$, $AB = 800m$. So we have:
$
   \Rightarrow AD + DB = AB, \\
   \Rightarrow x + DB = 800, \\
   \Rightarrow DB = 800 - x .....(iv) \\
$
Next, consider $\Delta ADC$,
$ \Rightarrow \tan {60^ \circ } = \dfrac{{CD}}{{AD}},$
We know that $\tan {60^ \circ } = \sqrt 3 $ and from equation $(ii)$ and $(iii)$, $CD = h$ and $AD = x$. Putting these values in above equation:
$
   \Rightarrow \sqrt 3 = \dfrac{h}{x}, \\
   \Rightarrow x = \dfrac{h}{{\sqrt 3 }} .....(v) \\
$
Now consider $\Delta BDC$,
$ \Rightarrow \tan {30^ \circ } = \dfrac{{CD}}{{BD}}$
We know that $\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$ and from equation $(ii)$ and $(iii)$, $CD = h$ and $DB = 800 - x$. Putting these values in above equation:
$
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{800 - x}}, \\
   \Rightarrow 800 - x = h\sqrt 3 \\
$
Putting $x = \dfrac{h}{{\sqrt 3 }}$ from equation $(v)$, we’ll get:
$
   \Rightarrow 800 - \dfrac{h}{{\sqrt 3 }} = h\sqrt 3 , \\
   \Rightarrow h\left( {\sqrt 3 + \dfrac{1}{{\sqrt 3 }}} \right) = 800, \\
   \Rightarrow h\left( {\dfrac{{3 + 1}}{{\sqrt 3 }}} \right) = 800, \\
   \Rightarrow h = \dfrac{{800\sqrt 3 }}{4}, \\
   \Rightarrow h = 200\sqrt 3 \\
$
Thus, the height of the bridge above the top of the temple is $200\sqrt 3 $ meters.

Note: Whenever angle of elevation or angle of depression is given, we use to analyse the scenario using a right angled triangle with the help of suitable trigonometric ratios depending upon what is given and what is asked in the question.