Question

A boy is standing on a cart moving along the\[x - \] axis with a speed of \[10\,{\text{m}}{{\text{s}}^{ - 1}}\] . When the cart reaches the origin, he throws a stone in the horizontal \[x - y\] plane, with a speed of \[5\,{\text{m}}{{\text{s}}^{ - 1}}\] with respect to himself at an angle \[\theta \] with the \[x - \] axis. It is found that the stone hits a ball lying at rest at a point whose coordinates are \[\left( {\sqrt 3 \,{\text{m}},\,1\,{\text{m}}} \right)\] . The value of \[\theta \] is (gravitational effects are to be ignored).
(A) \[30^\circ \]
(B) \[60^\circ \]
(C) \[90^\circ \]
(D) \[120^\circ \]

Answer 1

Hint: First of all, we will find the horizontal and vertical components of the velocity of the ball. Then we will find out the expression for vertical and horizontal distances using the components of velocities and the coordinate point given. We will manipulate the two expressions accordingly and obtain the result.

Complete step by step answer:
In the given question, we are supplied the following data:
The velocity of the boy is \[10\,{\text{m}}{{\text{s}}^{ - 1}}\] who is moving along the \[x - \] axis.
The velocity with which he throws the ball is \[5\,{\text{m}}{{\text{s}}^{ - 1}}\] .
The boy throws the ball at an angle \[\theta \] with the \[x - \] axis.
The stone hits a ball which is at rest at a point with coordinates \[\left( {\sqrt 3 \,{\text{m}},\,1\,{\text{m}}} \right)\] .
We are asked to find the angle with the \[x - \] axis at which the stone was thrown.
To have a better understanding, we draw a simple diagram, as below:

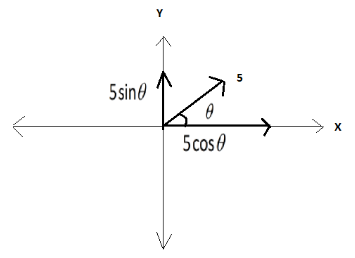
First, we will find the two components of the velocity of the stone.
Since, the velocity of the stone contains the velocity at which it was thrown and the velocity of the boy as well.
The horizontal component of the velocity is:
\[\Rightarrow{v_{\text{x}}} = \left( {10 + 5\cos \theta } \right)\,{\text{m}}{{\text{s}}^{ - 1}}\]
The vertical component of the velocity is:
\[\Rightarrow{v_{\text{y}}} = 5\sin \theta \]
The point at which the ball is \[\left( {\sqrt 3 \,{\text{m}},\,1\,{\text{m}}} \right)\] .
So, the horizontal distance is \[\sqrt 3 \,{\text{m}}\] and the vertical distance is \[1\,{\text{m}}\] .
By applying the formula which relates velocity, distance and time is:
\[\Rightarrow{\text{distance}} = {\text{velocity}} \times {\text{time}}\]……(1)
By substituting the required values (for the horizontal and vertical) in the equation (1), we get:
\[\Rightarrow\sqrt 3 = \left( {10 + 5\cos \theta } \right)t\] …… (2)
\[\Rightarrow 1 = \left( {5\sin \theta } \right) \times t\] …… (3)
Now, we divide the equation (2) by equation (3), and we get:
$
\Rightarrow\dfrac{{\sqrt 3 }}{1} = \dfrac{{10 + 5\cos \theta }}{{5\sin \theta }} \\
\Rightarrow 5\sqrt 3 \sin \theta = 10 + 5\cos \theta \\
\Rightarrow\sqrt 3 \sin \theta = 2 + \cos \theta \\
\Rightarrow\sqrt 3 \sin \theta - \cos \theta = 2 \\
$
Now, we divide the two sides by a factor \[2\]
$
\Rightarrow\dfrac{{\sqrt 3 }}{2}\sin \theta - \dfrac{1}{2}\cos \theta = 1 \\
\Rightarrow\sin \theta \cos \left( {\dfrac{\pi }{6}} \right) - \sin \left( {\dfrac{\pi }{6}} \right)\cos \theta = 1 \\
\Rightarrow \sin \left( {\theta - \dfrac{\pi }{6}} \right) = \sin \dfrac{\pi }{2} \\
\Rightarrow \theta - \dfrac{\pi }{6} = \dfrac{\pi }{2} \\
$
Simplifying again we get:
\[
\Rightarrow\theta = \dfrac{\pi }{2} + \dfrac{\pi }{6} \\
\Rightarrow\theta = \dfrac{{3\pi + \pi }}{6} \\
\Rightarrow\theta = \dfrac{{4\pi }}{6} \\
\Rightarrow\theta = \dfrac{{2\pi }}{3} \\
\Rightarrow\theta = 120^\circ
\]
Hence, the value of \[\theta \] is \[120^\circ \] .

The correct option is D.

Note: It is important to note that many students tend to make mistakes while finding the horizontal component of velocity. They just write \[5\cos \theta \] which is wrong, as the boy was also in motion while throwing the ball. His velocity must also be taken into account.