Question

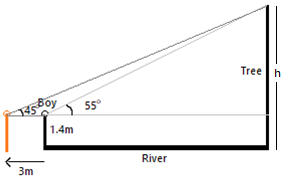
A boy, 1.4 metres tall standing at the edge of a river bank sees the top of a tree on the edge of the other bank at an elevation of ${{55}^{\circ }}$. Standing back by 3 metres, he sees it at an elevation of ${{45}^{\circ }}$.
a) Draw a rough figure showing these facts.
b) How wide is the river and how tall is the tree?
$\left[ \sin {{55}^{\circ }}=0.8192,\text{ }\cos {{55}^{\circ }}=0.5736,\text{ tan5}{{\text{5}}^{\circ }}=1.4281 \right]$

Answer 1

Hint: Such type of problem can easily be solved using sine and cosine of other angles as well. As the figure formed is a triangle, we can find out the other angle as one of the angles is ${{90}^{\circ }}$.

Complete step-by-step answer:
Here, as per the given conditions, a boy 1.4m tall is standing at the left-edge of the river bank, let’s say. And a tree of unknown height $h$, let’s say, on the right-edge of the river bank.
Boy makes an elevation of ${{55}^{\circ }}$ when he was at the edge, but when he moves 3m left side, he makes an elevation of ${{45}^{\circ }}$, thus, we have

Now, to calculate the height of tree and width of the river, we need to use triangle properties, i.e.,
Let’s say, $\Delta ABC$ is the required triangle having an elevation angle of ${{55}^{\circ }}$.

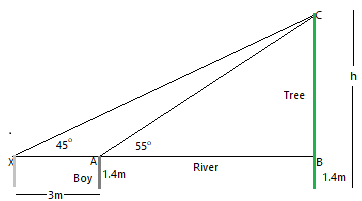
Now, let width of river be AB and height of tree be $h=BC+1.4$, thus
From $\Delta ABC$, we have
$\Rightarrow \tan \angle CAB=\dfrac{BC}{AB}$, where $BC=h-1.4$
$\Rightarrow \tan {{55}^{\circ }}=\dfrac{h-1.4}{AB}$
And from given values, $\tan {{55}^{\circ }}=1.4281$, thus
 $\begin{align}
  & \Rightarrow \tan {{55}^{\circ }}=\dfrac{h-1.4}{AB} \\
 & \Rightarrow 1.4281=\dfrac{h-1.4}{AB} \\
\end{align}$
Transposing values, we get
\[\begin{align}
  & \Rightarrow 1.4281=\dfrac{h-1.4}{AB} \\
 & \Rightarrow 1.4281\left( AB \right)=h-1.4 \\
 & \Rightarrow h=1.4281\left( AB \right)+1.4...\text{ }\left( 1 \right) \\
\end{align}\]
Similarly, for $\Delta XBC$, we have
$\Rightarrow \tan \angle CXB=\dfrac{BC}{BX}$ , where $BX=3+AB$ and $BC=h-1.4$
Thus,
$\begin{align}
  & \Rightarrow \tan {{45}^{\circ }}=\dfrac{BC}{BX} \\
 & \Rightarrow 1=\dfrac{h-1.4}{AB+3} \\
\end{align}$
Transposing values, we get
$\begin{align}
  & \Rightarrow 1=\dfrac{h-1.4}{AB+3} \\
 & \Rightarrow AB+3=h-1.4 \\
 & \Rightarrow h=AB+3+1.4 \\
 & \Rightarrow h=AB+4.4...\text{ }\left( 2 \right) \\
\end{align}$
Now, from equation (1) and (2), we get
$\begin{align}
  & \Rightarrow 1.4281\left( AB \right)+1.4=AB+4.4 \\
 & \Rightarrow \left( 1.4281-1 \right)AB=4.4-1.4 \\
 & \Rightarrow 0.4281\left( AB \right)=3 \\
\end{align}$
On cross-multiplication, we get
$\begin{align}
  & \Rightarrow 0.4281\left( AB \right)=3 \\
 & \Rightarrow AB=\dfrac{3}{0.4281} \\
 & \Rightarrow AB=7.007m \\
\end{align}$
Thus, from equation (2), we get
\[\begin{align}
  & \Rightarrow h=AB+4.4 \\
 & \Rightarrow h=7.007+4.4 \\
 & \Rightarrow h=11.407m \\
\end{align}\]
Hence, from both of the above equations, height of tree = $h=11.407m$ and width of river = $AB=7.007m$.

Note: A prominent mistake which can be made here is consideration of the boy as a point object, as we will be considering the top and bottom of the tree as a point. Also, as a boy is standing up straight, his height can be added on AB to calculate the height of the tree. Similarly, for the width of the river, distance the boy moved backwards can be used.