Question

A body weighing $ 0.4kg $ is whirled in a vertical circle with a string making 2 revolutions per second. If the radius of the circle is $ 1.2m $ . Find the tension (a) at the top of the circle, (b) at the bottom of the circle. Given; $ g = 10m{s^{ - 2}} $ and $ \pi = 3.14 $

Answer 1

Hint In a vertical circle, the weight of the body affects the tension on the string. At the top the weight provides some of the centripetal force required for circular motion. At the bottom, it increases the centripetal force required. So we need to set the equation for the body and from there we can calculate the tension in the string.
Formula used: In this solution we will be using the following formula;
 $ \Rightarrow {F_{NET}} = ma $ , where $ {F_{NET}} $ is the net force acting on a body, $ m $ is the mass of the body, and $ a $ is the acceleration attained by the body.
 $ \Rightarrow {a_c} = m{\omega ^2}r $ , where $ {a_c} $ is the centripetal acceleration of a body moving in a circular motion, $ \omega $ is the magnitude of the angular velocity of the body and $ r $ is the radius of the circle.

Complete step by step answer

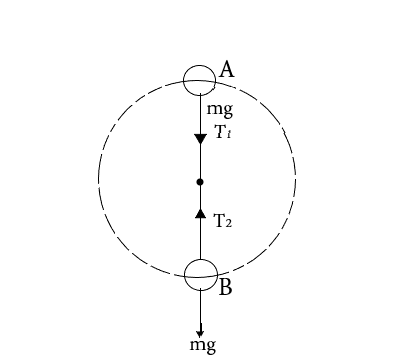
During a vertical swirl, the weight of the object plays an important role in the determination of the tension on the string. Depending on the immediate location of the body, it can either add to tension or relieve it. To calculate the tension, we analyse the motion using Newton’s second law of motion. Thus,
 $ \Rightarrow {F_{NET}} = ma $ where $ {F_{NET}} $ is the net force acting on a body, $ m $ is the mass of the body, and $ a $ is the acceleration attained by the body.
A) At point A on the vertical swirl (top if the circle):
 $ \Rightarrow {T_1} + mg = m{a_c} $ where $ T $ is the tension, $ g $ is the acceleration due to gravity, and $ {a_c} $ is the centripetal acceleration directed inward towards the centre of the circle.
Centripetal acceleration in general can be given as
 $ \Rightarrow {a_c} = m{\omega ^2}r $ where $ \omega $ is the magnitude of the angular velocity of the body and $ r $ is the radius of the circle.
According to the question, $ \omega = 2rev/s $ , converting to SI unit, we multiply by $ 2\pi $ (since 1 rev subtends $ 2\pi $ radians), hence
 $ \Rightarrow \omega = 12.56rad/s $ or $ \omega = 12.56{s^{ - 1}} $ .
Hence, we calculate $ m{a_c} $ from all known variables
 $ \Rightarrow m{a_c} = 0.4{\left( {12.56} \right)^2} \times 1.2 = 75.72N $
Hence,
 $ \Rightarrow {T_1} + 0.4\left( {10} \right) = 75.72 $
Thus,
 $ \Rightarrow {T_1} = 75.72 - 4 $
 $ \Rightarrow {T_1} = 71.72N $
B) For point B (bottom of circle)
 $ \Rightarrow {T_2} - mg = m{a_c} $ , (since tension and weight point in opposite direction)
Similarly,
 $ \Rightarrow {T_2} - 0.4\left( {10} \right) = 75.72 $
Thus,
 $ \Rightarrow {T_2} = 75.72 + 4 $
 $ \Rightarrow {T_2} = 79.72N $ .

Note
Alternatively we can calculate centripetal force from
 $ \Rightarrow m{a_c} = \dfrac{{m{v^2}}}{r} $ where $ v $ is the magnitude of the linear speed.
We calculate $ v $ from $ v = \omega r $ . Thus,
 $ \Rightarrow v = 12.56\left( {1.2} \right) = 15.072m/s $
 $ \Rightarrow m{a_c} = \dfrac{{0.4{{\left( {15.072} \right)}^2}}}{{1.2}} = 75.72 $ which is identical to the above.