Question

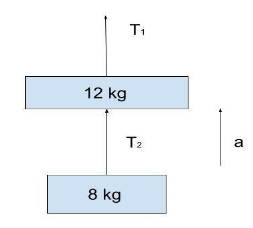
A body of mass $8\,kg$ is hanging from another body of mass $12\,kg$. The combination is being pulled up by a string with an acceleration of $2.2\,m/{\sec ^2}$. The tension ${T_{{1^{}}}}$ will be ?

Answer 1

Hint:In order to answer this question let us first go through pulley. Pulleys are wheel-and-rope devices that are used to carry large items to great heights. They can alter the direction of applied force and even reduce the amount of force required to lift a weight. Pulleys are sometimes used in buildings.

Complete step by step answer:
Tension is described as a pair of opposing forces acting at each end of the elements in question. A rope's tension force is felt by any segment of the rope in both directions, with the exception of the endpoints. The endpoints are subjected to friction on one side and force from the attached weight on the other. In certain cases, the stress varies across the string.
$T = mg$
where, $T$ is the tension, $m$= mass and $g$= gravitational force.

When two bodies move upwards with acceleration, gravity exerts a downward force i.e. ${\left( {{m_1} + {m_2}} \right)_g}$
According to Newton’s 2nd law
${T_1} = {\left( {{m_1} + {m_2}} \right)_g} = {\left( {{m_1} + {m_2}} \right)_a} \\
\Rightarrow {T_1} = \left( {{m_1} + {m_2}} \right) \times \left( {a + g} \right) \\
\Rightarrow {T_1} = \left( {12 + 8 \times } \right)\left( {2.2 + 9.8} \right) \\
\Rightarrow {T_1} = \left( {20} \right) \times \left( {12} \right) \\
\therefore {T_1} = 240\,N \\ $
Similarly,
${T_2} = {m_2}\left( {a + g} \right) \\
\Rightarrow {T_2} = 8 \times \left( {2.2 + 9.8} \right) \\
\Rightarrow {T_2} = 8 \times 12 \\
\therefore {T_2} = 96\,N \\ $
Hence, according to the question the tension ${T_{{1^{}}}}$ will be $240\,N$.

Note:Now, you might wonder if the tension in a rope is always the same. If the rope's force isn't used to accelerate anything else, including itself, the tension in the rope remains constant. As a result, if it is kept taut between two points and has zero mass, the stress would be considered constant throughout.