Question

A block “B” is pushed momentarily along a horizontal surface with an initial velocity $v$ . If $\mu $ is the coefficient of friction between B and the surface, block B will come to rest after a time

(A) $\dfrac{v}{{g\mu }}$
(B) $\dfrac{{g\mu }}{v}$
(C) $\dfrac{g}{v}$
(D) $\dfrac{v}{g}$

Answer 1

Hint: We know that friction is a force that resists the relative motion of a body on a surface. There are majorly two types of friction: static friction and Kinetic friction (also called sliding friction). Static friction occurs between two bodies that are relatively at rest, while kinetic friction occurs when the two bodies are in motion relative to each other. The coefficient of friction is a dimensional scalar quantity that represents the ratio of friction between the two bodies.
Formulas used: We will be using the formula $f = \mu N$ where $f$ is the frictional force acting on a body, $\mu $ is the coefficient of friction of the body, $N$ is the normal force acting on the body.
We will also be using the formula from equations of motion, $v = u + at$ where $v$ is the initial velocity of the body, $u$ is the final velocity of the body, $a$ is the acceleration of the body and $t$ is the time taken by the body to achieve the acceleration.

Complete Step by Step answer:
We know that friction is an opposing force that opposes the motion of the body, that is if a body is in motion due to a force, the frictional force is always acting on the body in a direction opposite to the direction of the motion. A body may or may not come to rest due to friction based on the intensity of friction.
From the problem we can infer that the initial velocity of the block is $v$ and it is about to come to rest due to the influence of frictional force acting on the body which has a frictional coefficient of $\mu $

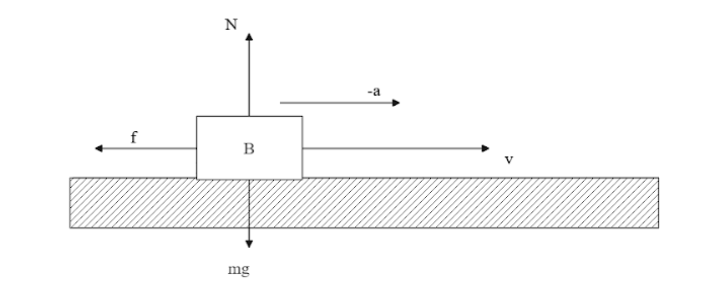
We know that a body always has gravitational pull towards the earth and a force that opposes the gravitational pull called the normal force acting opposite to it. We also know that friction is opposing the motion of the body and influencing it to come to rest. Thus, the body is decelerating in the direction of motion.
Now the frictional force acting on the body will be, $f = \mu N$. But considering the mass of the block is $m$ we know that the normal force on the body is $N = mg$ . Substituting the value of normal force to find frictional force on the body we get,
$f = \mu mg$ .
If the body is decelerating with respect to the frictional force, this means that the direction of acceleration is opposite to the direction of motion. So, we can say that the direction of acceleration is in the direction of friction. Now with respect to the frictional force acting on the body, we know $F = ma$ which can be written as, $f = ma$ . Substituting the value of frictional force,
$\mu mg = ma$
$ \Rightarrow a = \dfrac{{\mu mg}}{m} = \mu g$
Now that we know the acceleration of the body, let us apply the equations of motion on the body. Using $v = u + at$ with respect to the direction of motion we get,
$v = u + \left( { - a} \right)t$
We know that the body will come to rest and the initial velocity is $v$ so,
$0 = v - at$
Substituting the value for $a$ ,
$v = \left( {\mu g} \right)t$
$ \Rightarrow t = \dfrac{v}{{\mu g}}$
Thus, the time at which the body would come to rest is $t = \dfrac{v}{{\mu g}}$

Hence the correct answer will be option A.

Note: In the above problem we have considered that no other force is acting on the body. However to balance the forces on the body usually we would use, $F + f = ma$ .