Question

A bird is sitting on a tree which is 80m high. The angle of elevation of a bird from a point on a ground is \[{{45}^{\circ }}\] then the bird flies away from the point of observation horizontally and remains at a constant height. After 2 sec the angle of elevation from the point of observation becomes \[{{30}^{\circ }}\]. Find the speed of the flying bird.

Answer 1

Hint: The rough figure that represents the given information is shown below.

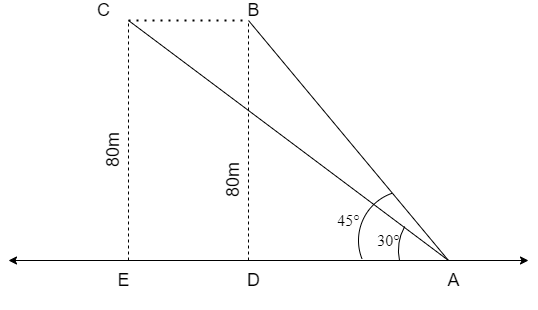
We solve this problem by using the simple formula of speed that is
\[\text{Speed}=\dfrac{\text{Distance}}{\text{time}}\]
For finding the distance we use the tangent trigonometric ratio formula that is
\[\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}\]
By using this formula we calculate the distance travelled by bird in 2 sec to find the speed.

Complete step-by-step answer:
We are given that the bird is initially at a height of 80m at position B.
So, from the figure we can say that
\[\Rightarrow BD=80m\]
Let us assume that the bird moves to point C after 2 sec.
We are given that the bird maintains a constant height.
So, we can say that
\[\Rightarrow CE=BD=80m\]
We know that the tangent trigonometric ratio formula that is
\[\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}\]
Now, let us consider the triangle \[\Delta ABD\]
Now, by applying the tangent trigonometric ratio formula we get
\[\Rightarrow \tan {{45}^{\circ }}=\dfrac{DB}{DA}\]
We know that from the standard table of trigonometric ratios we have
\[\tan {{45}^{\circ }}=1\]
Now, by substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow 1=\dfrac{80}{DA} \\
 & \Rightarrow DA=80 \\
\end{align}\]
Now, let us consider the triangle \[\Delta ACE\]
Now, by applying the tangent trigonometric ratio formula we get
\[\Rightarrow \tan {{30}^{\circ }}=\dfrac{CE}{EA}\]
We know that from the standard table of trigonometric ratios we have
\[\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}\]
Now, by substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{80}{EA} \\
 & \Rightarrow EA=80\sqrt{3} \\
\end{align}\]
We know that from the figure the length ‘ED’ can be written as
\[\Rightarrow ED=EA-DA\]
Now, by substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow ED=80\sqrt{3}-80 \\
 & \Rightarrow ED=80\left( \sqrt{3}-1 \right) \\
\end{align}\]
We are given that the bird maintain a constant height so, we can say that
\[\Rightarrow BC=ED=80\left( \sqrt{3}-1 \right)\]
Let us assume that the speed of bird as \['v'\]
We are given that the bird reaches point C after 2 sec so, we can take the time as
\[\Rightarrow t=2\]
We know that the formula of speed that is
\[\text{Speed}=\dfrac{\text{Distance}}{\text{time}}\]
By using the above formula we get the speed of bird as
\[\Rightarrow v=\dfrac{BC}{t}\]
Now, by substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow v=\dfrac{80\left( \sqrt{3}-1 \right)}{2} \\
 & \Rightarrow v=40\left( \sqrt{3}-1 \right) \\
\end{align}\]
Therefore the speed of bird is \[40\left( \sqrt{3}-1 \right){}^{m}/{}_{s}\]

Note: Students may make mistakes for trigonometric ratio formula.
We have the tangent trigonometric ratio formula that is
\[\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}\]
This formula is applicable only when the triangle is right angled triangle. But, students may use this formula for all types of triangles which is a blunder mistake.
So, the formula significance needs to be taken care of.