Question

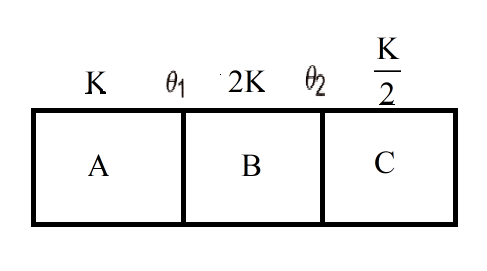
A, B and C are three identical conductors but made from different materials. But they are kept in contact as shown. Their thermal conductivity are \[{{K}}\], \[{{2K}}\]and\[\dfrac{{{K}}}{2}\]. The free end of A is at \[{100^\circ }{{C}}\] and the free end of C is at \[{0^\circ }{{C}}\]. During steady-state, the temperature of junction of A and B is nearly

(A) \[71^\circ {\text{C}}\]
(B) \[29^\circ {\text{C}}\]
(C) \[63^\circ {\text{C}}\]
(D) \[37^\circ {\text{C}}\]

Answer 1

Hint: The heat current passing through three conductors connected in the series arrangement with respect to each other of thermal conductivity\[{{K}}\], \[{{2K}}\] and \[\dfrac{{{K}}}{2}\] respectively is same.

Formula used:
Write the expression for the Heat resistance for conductor\[R\],
\[R = \dfrac{L}{{KA}}\]
Here, \[L\] is the inductive resistance, \[K\] is the thermal conductivity of the first conductor and \[A\] is the area.
Write the expression for the heat current in all three of the conductors.
\[i = \dfrac{{100 - {\theta _1}}}{{{R_1}}} = \dfrac{{{\theta _1} - {\theta _2}}}{{{R_2}}} = \dfrac{{{\theta _2} - 0}}{{{R_3}}}\]
Here \[i\] is the heat current throughout the conductors, \[{\theta _1}\] is the temperature at the junction of A and B and \[{\theta _2}\] is the temperature at the junction of B and C.

Complete step by step answer:
Write the expression for the Heat resistance for first conductor\[{R_1}\],
\[\
  {R_1} = \dfrac{L}{{KA}} \\
   = {R_0} \\
\ \]
Here, \[L\] is the inductive resistance, \[K\] is the thermal conductivity of the first conductor and \[A\] is the area.
Write the expression for the Heat resistance for second conductor\[{R_2}\],
\[\
  {R_2} = \dfrac{L}{{2KA}} \\
   = \dfrac{{{R_0}}}{2} \\
\ \]
Write the expression for the Heat resistance for Third conductor\[{R_3}\],
\[\
  {R_3} = \dfrac{{2L}}{{KA}} \\
   = 2{R_0} \\
\ \]
Understand that, the heat current throughout the conductor remains the same. Write the expression for the heat current in all three of the conductors.
\[i = \dfrac{{100 - {\theta _1}}}{{{R_1}}} = \dfrac{{{\theta _1} - {\theta _2}}}{{{R_2}}} = \dfrac{{{\theta _2} - 0}}{{{R_3}}}\]
Here \[i\] is the heat current throughout the conductors, \[{\theta _1}\] is the temperature at the junction of A and B and \[{\theta _2}\] is the temperature at the junction of B and C.
Substitute\[{R_0}\]for\[{R_1}\], \[\dfrac{{{R_0}}}{2}\] for\[{R_2}\], \[2{R_0}\] for \[{R_3}\]
\[\dfrac{{100 - {\theta _1}}}{{{R_0}}} = \dfrac{{2\left( {{\theta _1} - {\theta _2}} \right)}}{{{R_0}}} = \dfrac{{{\theta _2} - 0}}{{2{R_0}}}\]
Simplify the above equation
\[\left( {200 - 2{\theta _1}} \right) = \left( {4{\theta _1} - 4{\theta _2}} \right) = {\theta _2}\]
Consider the equation from second term and last term
\[\left( {4{\theta _1} - 4{\theta _2}} \right) = {\theta _2}\]
Rearrange
\[{\theta _2} = \dfrac{4}{5}{\theta _1}\]
Consider the equation from first and second term,
\[\left( {200 - 2{\theta _1}} \right) = \left( {4{\theta _1} - 4{\theta _2}} \right)\]
Rearrange,
\[6{\theta _1} - 4{\theta _2} = 200\]
Substitute \[\dfrac{4}{5}{\theta _1}\] for \[{\theta _2}\]
\[6{\theta _1} - 4\left( {\dfrac{4}{5}{\theta _1}} \right) = 200\]
Solve for \[{\theta _1}\]
\[\
  14{\theta _1} = 1000 \\
\Rightarrow {\theta _1} = 71.42 \\
 \approx 71 \\
\ \]

So, the correct answer is “Option A”.

Note:
The value of the heat resistance of three conductors are calculated using the expression for heat resistance of the conductor. Heat current expressions for all the conductors are equated to find out the equations of the temperature at junction points.