Question

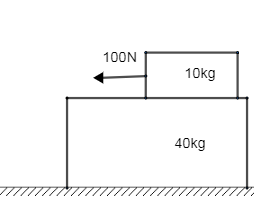
A 40kg slab rests on the frictionless floor. A 10kg block rests on top of the slab. The coefficient of the friction between the block and the slab is 0.40. The 10kg block is acted upon by a horizontal force of 100N. If$g=10m/{{s}^{2}}$, the resulting acceleration of the slab will be:

$\begin{align}
  & A.\text{ }1.0m/{{s}^{2}} \\
 & B.\text{ }1.47m/{{s}^{2}} \\
 & C.\text{ }1.52m/{{s}^{2}} \\
 & D.\text{ }6.1m/{{s}^{2}} \\
\end{align}$

Answer 1

Hint: We have been provided a block, placed over a slab. This whole thing is on the plane surface. We have been provided with a coefficient of friction (μ) and the mass of the slab and the block. To calculate acceleration of the slab, calculate friction force between slab and the block. To calculate friction force, resolve forces on the block by using a free body diagram. The acceleration provided to the slab is by friction force. Now resolve the force on the slab using the free body diagram. Equate friction force and the weight act on slab and hence calculate acceleration.

Complete answer:
We have been provided with the slab and the block of the mass 40kg and 10kg. The slab and the block are placed on one another. The block is acted by the horizontal force of 100N. Now we need to calculate the resulting acceleration of the slab.

To resolve the forces on the block, let’s draw the free body diagram of the block of the mass 10kg.

As you can see in the figure, force mg is balance by the normal force N and the static friction is balance by the force (F)
Mathematically,
N =mg
We know that kinetic friction is given by,
$f={{\mu }_{s}}N$
Where, ${{\mu }_{s}}$= coefficient of the friction.
We have been provided with the coefficient of the friction between the block and the slab is 0.40 i.e. ${{\mu }_{s}}$= 0.40
$f=0.4\times mg=0.4\times 10\times 10=40N$
Hence, kinetic friction of the block is 40N.
We have to calculate the acceleration of the slab. For that we need to find which forces are acting on the slab. So the free body diagram of the slab is given as follows,

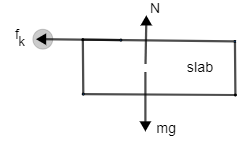
Force acting on the slab:
Normal N in upwards direction acting because of the ground weight mg in downwards direction, because of the gravity so as you can see, normal reaction is balancing weight mg.
Mathematically,
N = mg
Acceleration provided to slab is because of the kinetic friction between block and the slab according to Newton's law every action has equal and opposite reaction direction of the friction will be provided acceleration to the slab.
So, ${{f}_{k}}=Ma$
Mass of the slab (M) is 40kg, we get
$\begin{align}
  & 40=40a \\
 & a=1m/{{s}^{2}} \\
\end{align}$
Hence reusing acceleration of the slab will be $1m/{{s}^{2}}$.

Note:
Here, $1m/{{s}^{2}}$ is the acceleration by which the slab will move in the right direction. Friction acting is block and the slab is kinetic friction kinetic friction also between two bodies in contact, when one body is sliding over the other. There are three kinds of friction. Static friction acts between two bodies in contact when one body just moves or trends to move over the other. Rolling friction acts between two bodies in contact, when one body is rolling over the other.