Question

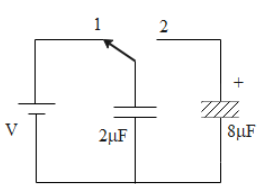
A 2 $\mu F$ capacitor is charged as shown in the figure. The percentage of its stored energy dissipated after the switch S is turned to position 2 is

$
  {\text{A}}{\text{. 0% }} \\
  {\text{B}}{\text{. 20% }} \\
  {\text{C}}{\text{. 75% }} \\
  {\text{D}}{\text{. 80% }} \\
$

Answer 1

Hint: First, we need to find out the initial energy stored in the \[2\mu F\] capacitor. Then we need to find out the final energy stored in the capacitors after the switch is turned to position 2. Then comparing these energies, we can get the required percentage of energy dissipated.
Formula used:
The energy stored in a capacitor having capacitance C and voltage V is given as
$U = \dfrac{1}{2}C{V^2}$

Complete answer:
In the given diagram when the switch S is connected to position 1 then the charging of the \[2\mu F\] capacitor will take place through the attached battery. This initial energy stored in the capacitor is given as
${U_i} = \dfrac{1}{2} \times 2 \times {V^2} = {V^2}$
Now when the switch S is connected to position two then the total voltage V will be shared between the two capacitors as the $2\mu F$ capacitor will start discharging while the $8\mu F$ capacitor will start getting charged. In this case the final voltage on $2\mu F$ capacitor is given as
${V_f} = \dfrac{{2\mu F}}{{2\mu F + 8\mu F}} \times V = \dfrac{V}{5}$
Now the total energy stored in the system of two capacitors will be
${U_f} = \dfrac{1}{2}\left( {2\mu F + 8\mu F} \right)V_f^2 = 5 \times \dfrac{{{V^2}}}{{25}} = 0.2{V^2}$
Now we can calculate the energy dissipated by dividing the change in energy with the initial energy and multiplying with 100 to get value in percentage.
Therefore, the percentage energy dissipated $ = \dfrac{{{V^2} - 0.2{V^2}}}{{{V^2}}} \times 100\% = 0.8 \times 100\% = 80\% $
This is the required value.

Hence, the correct answer is option D.

Note:
1. It should be noted that 80$\% $ dissipation in energy means that the second capacitor has taken up 80$\% $ of the energy of the first capacitor.
2. The energy is stored in a capacitor in the form of charge. The expression of energy stored can be given in the form of charge by using the relation $Q = CV$. The expression for energy stored in a capacitor becomes
$U = \dfrac{{{Q^2}}}{{2C}}$