Question

A $15\mu F$ capacitor is connected to a 220V, 50Hz source. Find the capacitive reactance and the current (rms and peak) in the circuit. If the frequency is doubled, what happens to the capacitive reactance and the current?

Answer 1

Hint: At first we need to look at the problem carefully and extract all the important values that are given. Now we have specific formulas for each of the values that the question wants. We have to wire the respective formulas and calculate the answer. For the second part of the question we will have to find a relation between capacitive reactance frequency and current and then we have to do a proportionality check which will give us the value of the capacitive reactance and current.
Formula Used:
${{X}_{c}}=\dfrac{1}{\omega c}$
${{X}_{c}}=\dfrac{1}{\left( 2\pi f \right)c}$
$\omega =2\pi f$
${{I}_{\circ }}=\sqrt{2}{{I}_{rms}}$
${{I}_{rms}}=\dfrac{{{V}_{rms}}}{Z}$

Complete answer:

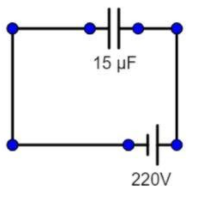
Here we can see the diagram of the circuit that is given in the question all the capacitors and sources of current are shown in it.
So we know that, according to the question, there is a capacitor of capacitance $15\mu F$ or$15\times {{10}^{-6}}F$ .
And the capacitor is connected to a ${{V}_{rms}}=220V$supply, which has a source of $f=50Hz$ .
We have to find the capacitive reactance and the current in the circuit when the frequency is normal and when it is doubled.
We know the formula for capacitive reactance,
${{X}_{c}}=\dfrac{1}{\omega c}$ or ${{X}_{c}}=\dfrac{1}{\left( 2\pi f \right)c}$ as $\omega =2\pi f$
So, now putting the values given in the equation,
${{X}_{c}}=\dfrac{1}{\left( 2\times \dfrac{22}{7}\times 50 \right)\times 15\times {{10}^{-6}}}$ ,
$\Rightarrow {{X}_{c}}=\dfrac{7\times {{10}^{4}}}{22\times 15}$
On solving the above equation we get,
\[{{X}_{c}}=212\Omega \] this is actually the capacitive reactance of the circuit.
Now, we know the formula for rms value of current,
${{I}_{rms}}=\dfrac{{{V}_{rms}}}{Z}$
Now, putting in the values,
$\Rightarrow {{I}_{rms}}=\dfrac{220}{212}A$($z={{X}_{c}}$)
On solving the above equation we will get,
$\Rightarrow {{I}_{rms}}=1.04A$this is the rms value of current in the circuit.
Now, we know the formula for peak value of current,
${{I}_{\circ }}=\sqrt{2}{{I}_{rms}}$
On putting in the values,
$\Rightarrow {{I}_{\circ }}=1.414\times 1.04A$
So on calculating the above equation we get,
$\Rightarrow {{I}_{\circ }}=1.47A$this is the peak value of current in the circuit.
Now, it is asked that if the frequency is doubled what will be the consequences in the circuit, So we know that capacitive reactance is inversely proportional to frequency and current I is also inversely proportional to capacitive reactance. So, if the frequency is doubled then the capacitive reactance will be halved and if it is halved then the current will be doubled.

Note:
In the equation ${{X}_{c}}=\dfrac{1}{\omega c}$,$\omega $ here is the angular frequency, ‘c’ is the capacitance of the capacitor. And in the equation ${{I}_{rms}}=\dfrac{{{V}_{rms}}}{Z}$, ‘z’ is actually the impedance of the circuit. Students must remember all the formulas and relationships between the properties of the circuit properly to solve the question.