Question

3 cubes of edge $4\text{cm}$ are joined end to end. Find the surface area of the resulting cuboid.

Answer 1

Hint: The side of the cube is given in the question. With the help of the side of the cube, we will find the dimensions of the resulting cuboid. Then to find the surface area of the resulting cuboid,we will use the expression of the surface area of the cuboid. We will substitute the value of length, breadth and height in the expression of the surface area of the cuboid to get the final answer.

Complete step-by-step answer:
The surface area of the cuboid is expressed as:
 $S\text{urface area of cuboid}=2\left(lb+bh+hl\right)$
Here $l$ stand for length, $b$ stands for breadth and $h$ stands for height.
Step by step answer:
The side of the three cubes is $\text{4}\text{cm}$ . It is given in question that we need to join three cubes. It can be shown as:

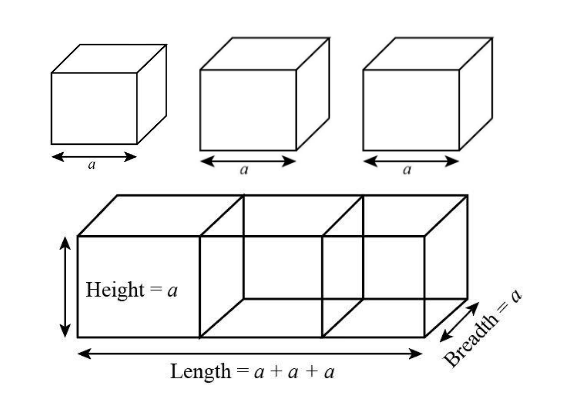
We can see that from the figure that after joining two cubes, one cuboid will fotext whose side can be expressed as
The length of the cuboid is:
$\begin{array}{l}l=a+a+a\\ l=4\text{cm}+4\text{cm}+4\text{cm}\\ l=12\text{cm}\end{array}$
The breadth of the cuboid is $b=a=4\text{cm}$
The height of the cuboid is $h=a=4\text{cm}$
We know that the surface area of the cuboid can be expressed as
 $S\text{urface area of cuboid}=2\left(lb+bh+hl\right)$
 We will substitute $12\text{cm}$ for $l$ , $4\text{cm}$ for $b$ and $4\text{cm}$ for $h$ in the above expression, we will get
 $\begin{array}{l}S\text{urface area of cuboid}=2\left(\left(12\text{cm}\right)\left(4\text{cm}\right)+\left(4\text{cm}\right)\left(4\text{cm}\right)+\left(4\text{cm}\right)\left(4\text{cm}\right)\right)\\ S\text{urface area of cuboid}=2\left(48\text{c}{\text{m}}^2+16\text{c}{\text{m}}^2+32\text{c}{\text{m}}^2\right)\\ S\text{urface area of cuboid}=2\left(96\text{c}{\text{m}}^2\right)\\ S\text{urface area of cuboid}=192\text{c}{\text{m}}^2\end{array}$
 Hence the surface area of the resulting cuboid is $\text{192}\text{c}{\text{m}}^{\text{2}}$ .

Note: Whenever we join three cubes, a new cuboid is fotexted such that the volume never changes but the surface area always changes. The volume of the three cubes joined will always be equal to the volume of the cuboid. But we need to calculate the surface area as it always changes.