




Derivation and Formula for Magnetic Field at Center and Axis of Circular Loop
Understanding the Magnetic Field Due To A Current Through A Circular Loop is essential for grasping how electric currents create magnetic effects, a core topic in class 10 and 12 physics curriculums. This topic explains the underlying principles, formulae, derivations, and practical significance, helping students visualize and solve problems involving current-carrying loops. Explore this page to master the fundamental concepts and their real-world applications.
Explaining the Magnetic Field Due to a Current-Carrying Circular Loop
When electrical current flows through a conductor shaped into a circular loop, it creates a magnetic field around it. This field encircles the loop and is strongest at the center. According to the magnetic field due to a current through a circular loop definition, the region surrounding the loop where the force of magnetism acts is called the magnetic field. This concept is a key part of topics like magnetic field due to a current through a circular loop class 10 and magnetic field due to a current through a circular loop class 12, and is fundamentally related to magnetic effects of electric current.
If you observe the pattern of the magnetic field lines generated, you'll notice that they form concentric circles near the wire and become straight at the center of the loop. The direction of the magnetic field at any point around the loop can be determined using the Right Hand Thumb Rule (Maxwell’s Rule): if the right hand’s fingers curl in the direction of current flow around the loop, the thumb points to the direction of the magnetic field within the loop.
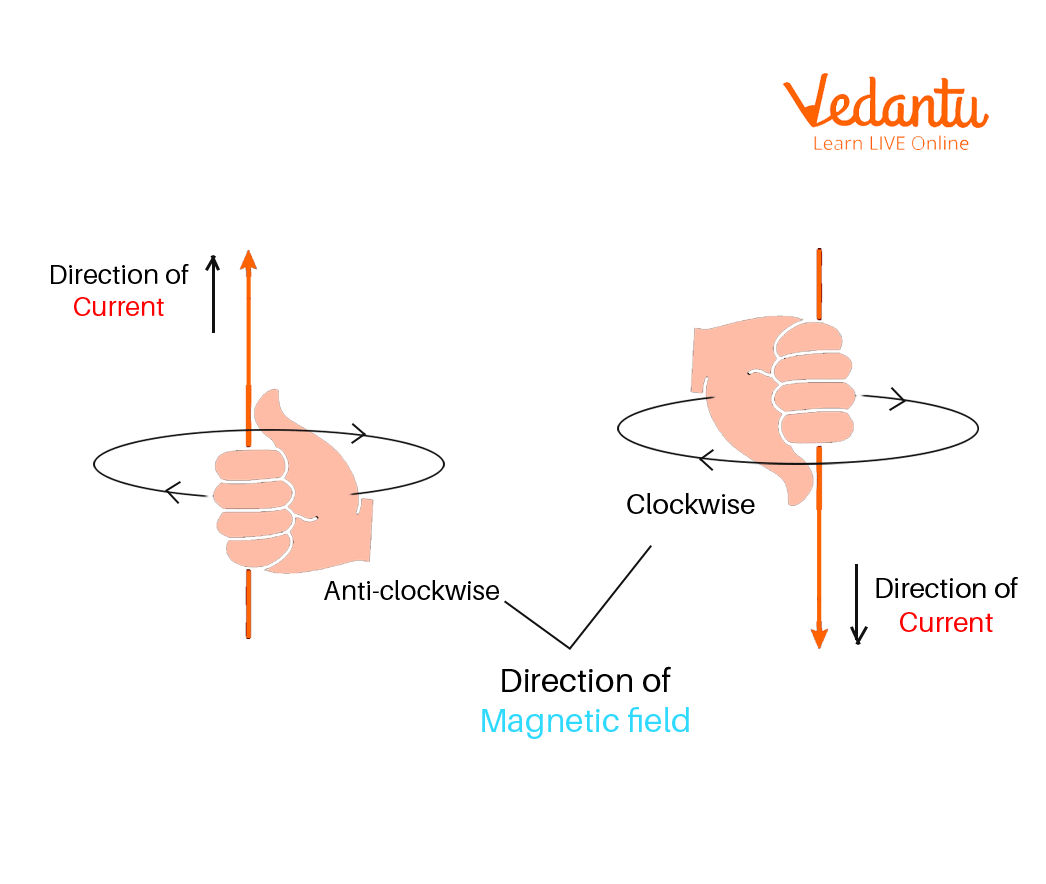
This principle can be further explored by examining simple experiments, such as placing a magnetic compass at various points around a current-carrying loop to observe deflection, or sprinkling iron filings to visualize the field pattern. The concept of attraction and repulsion between magnets is closely linked to these observations.
Key Formulas for the Magnetic Field of a Circular Loop
In topics such as magnetic field of a loop formula or magnetic field at the centre of a circular loop formula, the following equations are central:
- At the Center of the Loop: $B = \dfrac{\mu_0 I}{2R}$
- On the Axis of the Loop (distance $x$ from center): $B = \dfrac{\mu_0 I R^2}{2 (R^2 + x^2)^{3/2}}$
Here, $B$ is the magnetic field, $\mu_0$ is the permeability of free space, $I$ is the current, $R$ is the loop’s radius, and $x$ is the distance along the axis from the center. These formulas are also highlighted in magnetic field due to a current through a circular loop class 10 notes and class 12 notes.
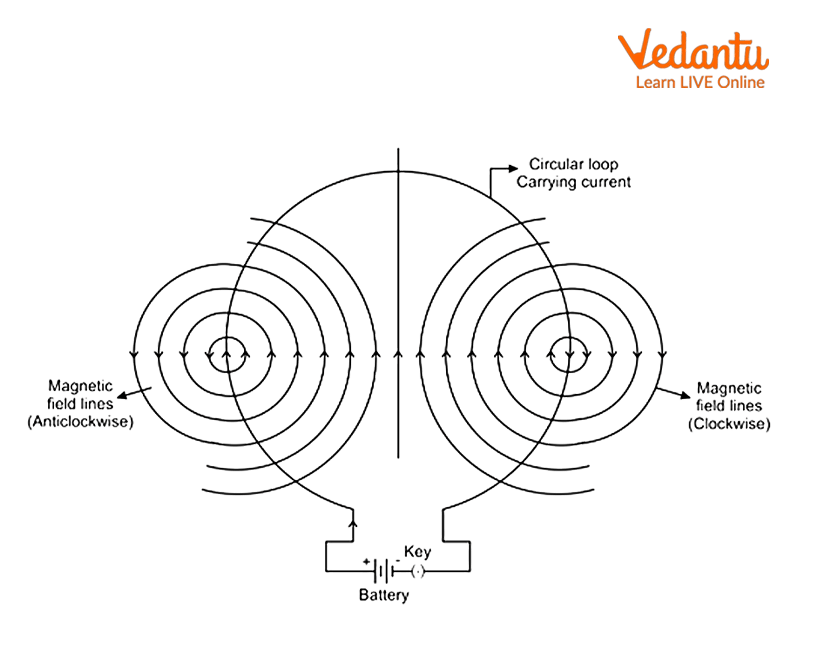
In the figure above—a typical magnetic field due to a current through a circular loop diagram—you can see how the field forms loops around the conductor and is densest at the center. Such diagrams are often used in exams to explain or derive relevant formulas.
Step-by-Step Derivation: Magnetic Field on the Axis of a Circular Loop
- Consider a circular loop of radius $R$ carrying current $I$. We want the magnetic field at a point $P$ lying at distance $x$ from the center on its axis.
- By the Biot–Savart Law, the magnetic field due to an infinitesimal segment $dl$ is $d\vec{B} = \dfrac{\mu_0}{4\pi} \dfrac{I (d\vec{l} \times \vec{r})}{r^3}$, where $r$ is the distance from $dl$ to $P$.
- For every segment, by symmetry, only the axial components (along $x$) sum up; radial components cancel.
- Summing over the entire loop and resolving geometry, $r = \sqrt{R^2 + x^2}$ and the $x$-component is scaled by $\cos \theta = \dfrac{x}{\sqrt{R^2 + x^2}}$.
- Adding up all infinitesimal $dB_x$ over $2\pi R$, the total magnetic field on axis is:
$B = \dfrac{\mu_0 I R^2}{2(R^2 + x^2)^{3/2}}$
Special Case—At the Centre ($x = 0$):
$B = \dfrac{\mu_0 I}{2R}$
This aligns with the magnetic field at the centre of a circular loop formula, a key snippet for quick reference.
Such derivations are a foundational part of magnetic field due to a current through a circular loop derivation in class 12 and are instrumental for tackling more advanced magnetic field problems.
Applications and Example Calculations
Circular loops are widely used in electromagnets, antenna designs, and laboratory instruments like galvanometers. Analyzing the magnetic field at different points is crucial for current-carrying loop technologies, as well as for experiments involving the superposition of fields from multiple loops.
Let's examine a sample calculation, similar to questions found in class 10 and class 12 physics exams:
- Example: A circular loop of radius $0.05$ m carries a current of $2$ A. What is the magnetic field at its center?
Apply $B = \dfrac{\mu_0 I}{2R}$ with $\mu_0 = 4\pi \times 10^{-7}$ T·m/A:
$B = \dfrac{4\pi \times 10^{-7} \times 2}{2 \times 0.05} = \dfrac{8\pi \times 10^{-7}}{0.1}$
$= 8\pi \times 10^{-6}$ T ≈ $2.51 \times 10^{-5}$ T
This approach is essential for practical applications and for understanding the core of magnetic flux in circular loops.
Summary Table: Key Quantities for Circular Current Loops
| Parameter | Symbol / Formula | Unit |
|---|---|---|
| Magnetic Field at Centre | $B = \dfrac{\mu_0 I}{2R}$ | Tesla (T) |
| Field on Axis (distance $x$) | $B = \dfrac{\mu_0 I R^2}{2(R^2 + x^2)^{3/2}}$ | Tesla (T) |
| Current | $I$ | Ampere (A) |
| Radius of Loop | $R$ | Meter (m) |
| Permeability of Free Space | $\mu_0$ | $4\pi \times 10^{-7}$ T·m/A |
These parameters are fundamental to analyzing and predicting the magnetic behavior of current-carrying loops and are building blocks in topics such as class 12 physics formulas and competitive exams.
Conclusion: Key Takeaways on Magnetic Field Due To A Current Through A Circular Loop
The magnetic field due to a current through a circular loop is a pivotal topic spanning class 10 and class 12, with applications ranging from basic lab devices to advanced electromagnetics. By mastering its definition, diagrams, formulas, and derivations, students can confidently approach both conceptual and numerical problems. For a more comprehensive understanding of related physics principles, review concepts like Biot–Savart Law, force in physics, and real-world applications found throughout advanced curricula. Continue exploring these connected ideas to deepen your awareness of electromagnetism’s impact on technology and science.
FAQs on Magnetic Field Produced by a Current-Carrying Circular Loop
1. What is the magnetic field due to a current through a circular loop?
The magnetic field produced by a current-carrying circular loop is strongest at the centre of the loop and depends on the current, radius, and number of turns.
Key points:
- The direction of the magnetic field follows the right-hand thumb rule.
- The strength increases with higher current and more turns.
- At the centre, the magnetic field (B) is given by:
B = (μ₀ * I * N)/(2R)
where μ₀ is the permeability of free space, I is current, N is number of turns, and R is radius. - Field lines are concentric circles near the wire and straight at the centre.
2. How is the direction of the magnetic field determined for a circular loop?
The direction of the magnetic field around a current-carrying circular loop is determined by the right-hand thumb rule.
To apply:
- Hold the loop in your right hand such that the curled fingers point in the direction of current flow.
- Your thumb, pointing through the centre of the loop, indicates the direction of the magnetic field inside the loop.
- The field forms closed loops, becoming perpendicular to the plane at the centre.
3. Why is the magnetic field at the centre of a circular loop stronger than at other points?
The magnetic field at the centre of a circular loop is strongest because the field due to all current elements adds up constructively at that point.
Important factors:
- Each segment of the wire produces a magnetic field at the centre pointing in the same direction.
- Fields reinforce each other at the centre but weaken as you move away.
- The field strength decreases with distance from the centre.
4. How can you increase the magnetic field produced by a circular loop?
The magnetic field produced by a circular loop can be increased by modifying certain factors.
Ways to increase the field:
- Increase the current through the loop (I).
- Increase the number of turns (N).
- Decrease the radius of the loop (R).
- Use a core with high permeability inside the loop, if possible.
5. What is the formula for the magnetic field at the centre of a current-carrying circular loop?
The magnetic field (B) at the centre of a current-carrying circular loop is given by:
- B = (μ₀ * I * N) / (2R)
- Here, μ₀ = permeability of free space (4π × 10⁻⁷ Tm/A)
- I = current, N = number of turns, R = radius of the loop
This formula shows direct proportionality with current and number of turns, and inverse with radius.
6. What is the shape and direction of magnetic field lines around a circular loop?
The magnetic field lines around a current-carrying circular loop are concentric circles near the wire and become almost straight at the centre of the loop.
Features include:
- Near the wire, lines circle the conductor.
- At the centre, lines add up to form a strong, straight field perpendicular to the plane of the loop.
- The direction is given by the right-hand thumb rule.
7. How does the number of turns in a circular coil affect the magnetic field strength?
The magnetic field strength at the centre of a circular coil increases with the number of turns.
Details:
- More turns (N) means greater total field, as B is directly proportional to N.
- If the same current passes through each turn, their individual fields add up at the centre.
8. What are the applications of magnetic field produced by a current-carrying circular loop?
The magnetic field generated by current-carrying circular loops is used in various practical applications.
Examples:
- Electromagnets for lifting heavy objects.
- Electric motors and generators.
- Measuring instruments like galvanometers.
- Induction coils and transformers.
9. What happens to the direction of the magnetic field if the current in the circular loop is reversed?
If the current direction in the circular loop is reversed, the direction of the magnetic field at the centre also reverses.
Key facts:
- The right-hand thumb rule shows the new field direction.
- The direction of field lines flips while the strength remains unchanged, provided current magnitude is constant.
10. Describe the magnetic field pattern as observed using iron filings for a circular loop carrying current.
When iron filings are sprinkled around a current-carrying circular loop, they arrange themselves to show the magnetic field pattern.
Main observations:
- Concentric circles are seen around the wire.
- At the centre, filings line up perpendicular to the plane of the loop, indicating a strong, uniform field.
- The pattern becomes less dense farther from the centre.
11. What is the right-hand rule for a current-carrying circular loop?
The right-hand rule helps determine the direction of the magnetic field produced by a current-carrying circular loop.
How to apply:
- Grasp the loop with your right hand so that your fingers point in the direction of current flow.
- Your thumb points in the direction of the magnetic field at the centre.
12. What factors determine the strength of the magnetic field at the centre of a circular loop?
The strength of the magnetic field at the centre of a current-carrying circular loop depends on multiple factors.
Important factors include:
- The magnitude of current (I) passing through the loop
- The number of turns in the coil (N)
- The radius of the loop (R)
- The permeability of the medium (μ₀)























