




How to Plot and Identify Whole Numbers on a Number Line
What do we call the set of natural numbers or counting numbers which include zero? The set of natural numbers or counting numbers that include zero is called whole numbers. These are represented by writing, N + {0}. Whole numbers serve as the pillar for learning the countings. In the writing below, children would understand the whole numbers, unknown facts about them, and the representation of whole numbers on the number line. So, let us begin with learning about this easiest and most interesting topic.
What Do You Mean by Whole Number?
All natural numbers and 0 are included in the category of whole numbers. In simple words, whole numbers are a set of numbers without fractions, decimals, or even negative integers. Whole numbers include counting numerals along with zero. The English alphabet W is used to denote the set of whole numbers. The bundle of whole numbers is represented as:
W = {0, 1, 2, 3, 4, ……}.
Whole Numbers on the Number Line
To represent the whole numbers on the number line, one needs to follow some steps, which are given below:
Draw a straight line of any length, called a number line.
Mark all the positive integers along with 0 excluding the negative integers
The set of numbers being shown on the number line represents the whole numbers on the number line(Blue coloured)
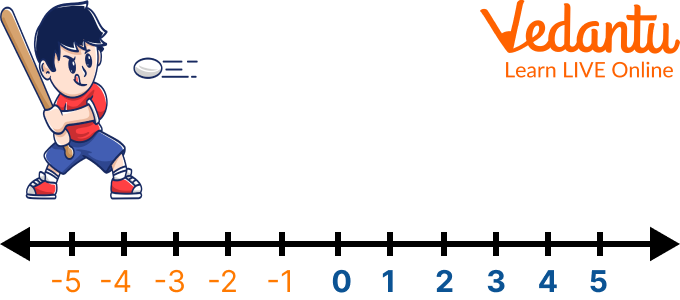
Showing the Representation of Whole Numbers on the Number Line
Addition of Whole Numbers on the Number Line
Follow the given series of steps for the addition of whole numbers on the number line:
Assume any of the given numbers as the starting point on the number line
Mark the point on the number line.
Now, jump as many units as equivalent to the other given number towards the right side from the starting point.
Mark the final point where you have reached after jumping.
This point gives the addition of two whole numbers on the number line.
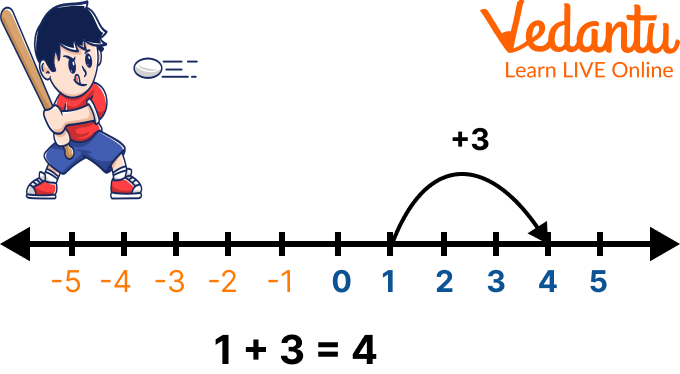
Addition of Two Whole Numbers on the Number Line
Facts About the Whole Numbers
Some facts about the whole numbers are discussed underneath:
Whole numbers make up all natural numbers.
Zero along with all the positive integers forms the whole numbers.
Real numbers consist of all the whole numbers along with other numbers.
Zero is the smallest whole number.
Whole numbers are not available in form of fractions.
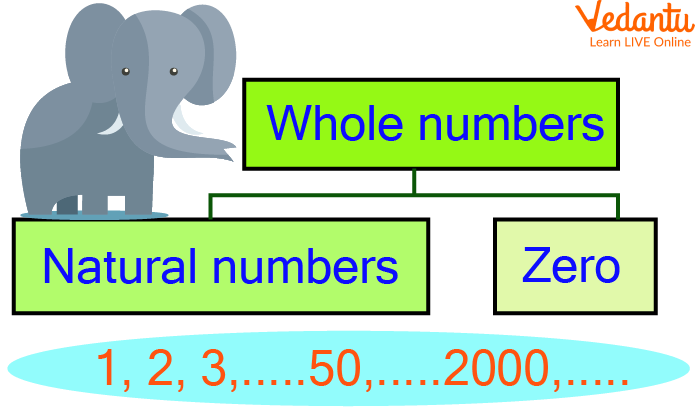
Showing the Whole Numbers
Solved Examples
Q 1. Add the whole numbers 5 and 7 using the number line.
Ans: Follow the given steps for performing the addition of whole numbers on the number line:
Assume any of the given numbers as the starting point on the number line, say 5
Mark the point 5 on the number line
Now, jump as many units as equivalent to the other given number, i.e. 7 towards the right side from the starting point, 5
Mark the final point, where you have reached i.e. 12
This point i.e. 12 gives the addition of two whole numbers, 5 and 7 on the number line.
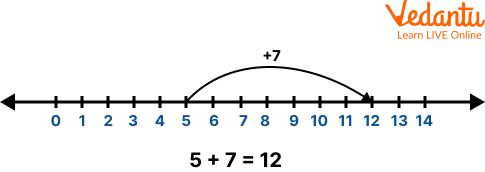
Showing the Addition of Whole Numbers on the Number Line
Q 1. Add the whole numbers 4 and 5 using the number line.
Ans: Follow the given steps for performing the addition of whole numbers on the number line:
Assume any of the given numbers as the starting point on the number line, say 4
Mark the point 4 on the number line
Now, jump as many units as equivalent to the other given number, i.e. 5 towards the right side from the starting point, 4
Mark the final point, where you have reached i.e. 9
This point i.e. 9 gives the addition of two whole numbers, 4 and 5 on the number line.
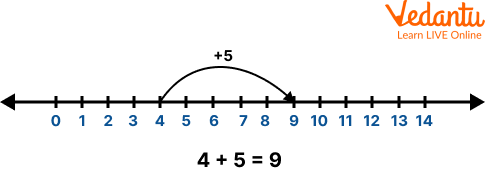
Showing the Addition of Whole Numbers on the Number Line
Practice Problems
Q 1. Identify and write the whole numbers from the given set
{1, 2, 3.5, -3, $\dfrac{5}{2}$, -7, 8}.
Ans. The whole numbers from the above set are 1, 2, and 8.
Q 2. What happens when a whole number is multiplied by zero?
Ans: The answer is zero.
Q 3. Add the given whole numbers by using the real line or number line.
2 and 4 (Ans: 6)
6 and 3 (Ans: 9)
Summary
Summing up here with the topic of the whole numbers. This article covers everything about whole numbers, starting from what do you mean by whole numbers to the representation of whole numbers on the number line. Every topic discussed in the article is presented in a simple language and to-the-point format. Some solved examples along with some practice problems are being assigned to students for a better understanding of the concepts. Sense autonomous to ask your doubts in the comments below.
FAQs on Whole Numbers on the Number Line: Explained with Examples
1. What is the main difference between natural numbers and whole numbers?
The primary difference is the inclusion of zero. Natural numbers are the counting numbers that start from 1 (1, 2, 3, ...). Whole numbers include all natural numbers plus the number zero (0, 1, 2, 3, ...). Therefore, every natural number is a whole number, but 0 is a whole number that is not a natural number.
2. How are whole numbers represented on a number line?
To represent whole numbers on a number line, you follow these steps:
- Draw a straight horizontal line.
- Mark a point on the far left and label it 0. This is the starting point for whole numbers.
- Mark points at equal intervals to the right of 0.
- Label these points sequentially as 1, 2, 3, 4, and so on.
The line extends indefinitely to the right, indicated by an arrow, showing that there is no largest whole number.
3. Can you give an example of adding two whole numbers, like 3 and 4, on a number line?
Yes. To add 3 + 4 on a number line, you would:
- Start at the point labelled 3.
- Move 4 units to the right, as addition means moving towards larger numbers.
- Each jump represents one unit. After four jumps from 3, you will land on the point labelled 7.
Therefore, the number line visually shows that 3 + 4 = 7.
4. Why does the number line for whole numbers start at 0 and extend only to the right?
The number line for whole numbers starts at 0 because 0 is the smallest whole number. The line extends only to the right because whole numbers do not include negative values. The numbers to the right of 0 represent all the positive integers (1, 2, 3,...), which, along with 0, make up the complete set of whole numbers. The space to the left of 0 is reserved for negative numbers, which are part of the integer system, not the whole number system.
5. On a number line, which whole number is to the left: 503 or 530?
The number 503 is to the left of 530 on the number line. On a standard number line, numbers increase in value as you move from left to right. Since 503 is a smaller value than 530, it will always be positioned to the left of 530.
6. Can we show subtraction of whole numbers on a number line? For example, 8 - 5.
Yes, subtraction can also be shown on a number line. While addition is a movement to the right, subtraction is a movement to the left. To calculate 8 - 5:
- Start at the point labelled 8.
- Move 5 units to the left (towards zero).
- After moving 5 units to the left from 8, you will land on the point labelled 3.
This demonstrates that 8 - 5 = 3. This only works if the result is a whole number.
7. What are the key properties of whole numbers as per the CBSE syllabus?
Whole numbers satisfy several key properties for addition and multiplication:
- Closure Property: Adding or multiplying two whole numbers results in a whole number (e.g., 2+3=5; 2x3=6).
- Commutative Property: The order of numbers doesn't affect the result (e.g., a+b = b+a; a×b = b×a).
- Associative Property: The grouping of numbers doesn't affect the result (e.g., (a+b)+c = a+(b+c)).
- Additive Identity: Adding 0 to any whole number gives the number itself (a + 0 = a).
- Multiplicative Identity: Multiplying any whole number by 1 gives the number itself (a × 1 = a).
- Distributive Property: Multiplication distributes over addition (e.g., a × (b+c) = a×b + a×c).
8. Since whole numbers don't include fractions, how do we acknowledge the space between 2 and 3 on a number line?
The space between any two consecutive whole numbers like 2 and 3 on a number line represents numbers that are not whole numbers. These include fractions (like 2 ½) and decimals (like 2.5). While these points exist on the physical line, they are not part of the set of whole numbers. This illustrates that the number line can be used to represent many different types of numbers, and whole numbers are just one specific set of points on it.
9. Is there a 'largest' whole number? Why or why not?
No, there is no 'largest' whole number. The set of whole numbers is infinite. For any whole number you can name, you can always find a larger one by simply adding 1 to it. This is why a number line for whole numbers has an arrow on the right side, signifying that the numbers continue forever.
10. What is the relationship between whole numbers and integers?
The set of integers is an extension of the set of whole numbers. Integers include all the whole numbers (0, 1, 2, 3, ...), as well as the negative counterparts of the natural numbers (..., -3, -2, -1). So, every whole number is an integer, but not every integer is a whole number. On a number line, integers extend infinitely in both the positive (right) and negative (left) directions from zero.

















