An Introduction to Equations for Line Parallel to X-Axis
In the coordinate plane, there is an infinity of points. A line traverses a point. Equations of horizontal and vertical lines and equations in point-slope, two-point, slope-intercept, intercept, and standard forms are examples of straight-line equations. In the following parts on this page, you can learn more about the equation of a line parallel to the x-axis and answer the question of which graph is parallel to the x-axis.
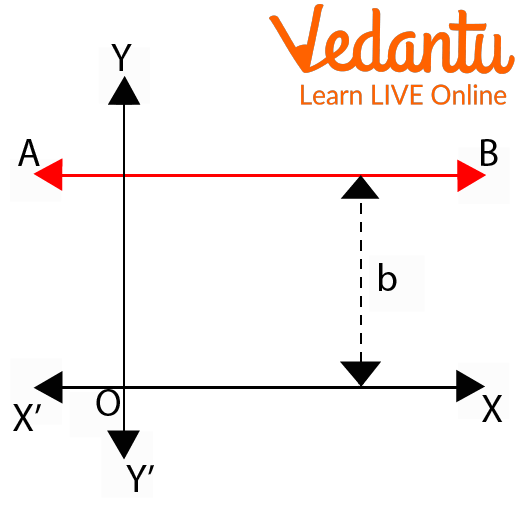
Line AB represents the Line Parallel to the x-axis
By the end of this article, we will be able to answer the equation of the x-axis, which graph is parallel to the x-axis, and which is parallel to the x-axis.
What is the Equation of the X-axis or Equation of Line Parallel to the X-axis?
Equations of the x-axis or equations representing the lines parallel to the x-axis are of the type y = a, where a is a constant value, and this line cuts the y-axis at the coordinates (0, a). If we represent this line on the graph, it will be perpendicular to the unit from the x-axis line.
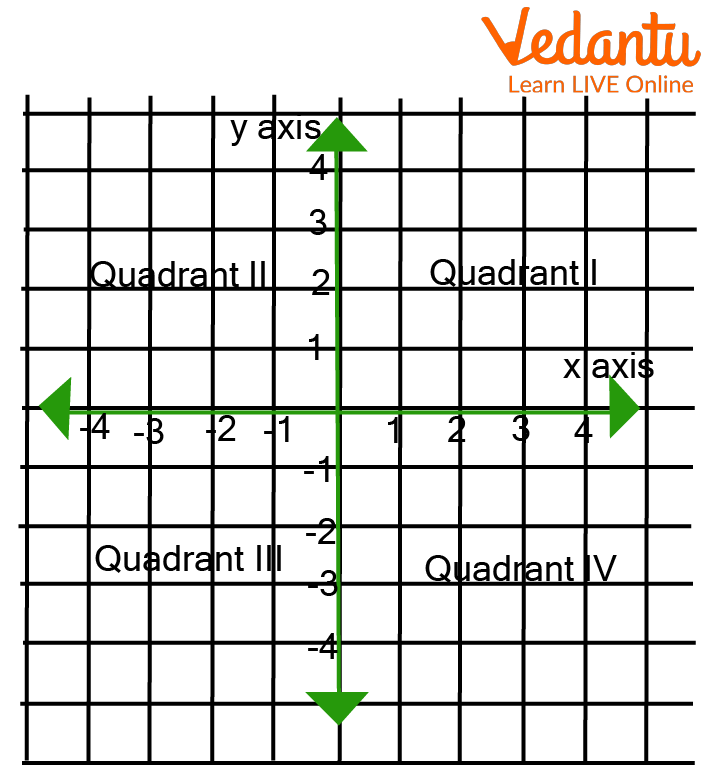
Cartesian Divided Into Four Quadrants
The equation of a line parallel to the x-axis in the positive y-axis always intersects through the 1st and the 2nd quadrant. At the same time, the equation of the line parallel to the x-axis in the negative y-axis intersects through the 3rd and the 4th quadrant of the coordinate axes.
Properties of the Equation of Line Parallel to the X-Axis
The following are the properties of the equation of the line parallel to the x-axis given:
The line parallel to the x-axis intersects the y-axis at one point.
Line parallel to x intersects y at only one point (0, a) and has the formula y = a.
The equation of line parallel to the x-axis and intersecting the y-axis at the point (0, a) is at an equidistance of 'a' units from the x-axis.
All points lying on the line parallel to the x-axis will have the same y coordinate
The slope of the line parallel to the x-axis will always be equal to zero.
Solved Examples
Example 1: Write the equations for the lines L1 and L3 out of the four equations as shown in the figure.
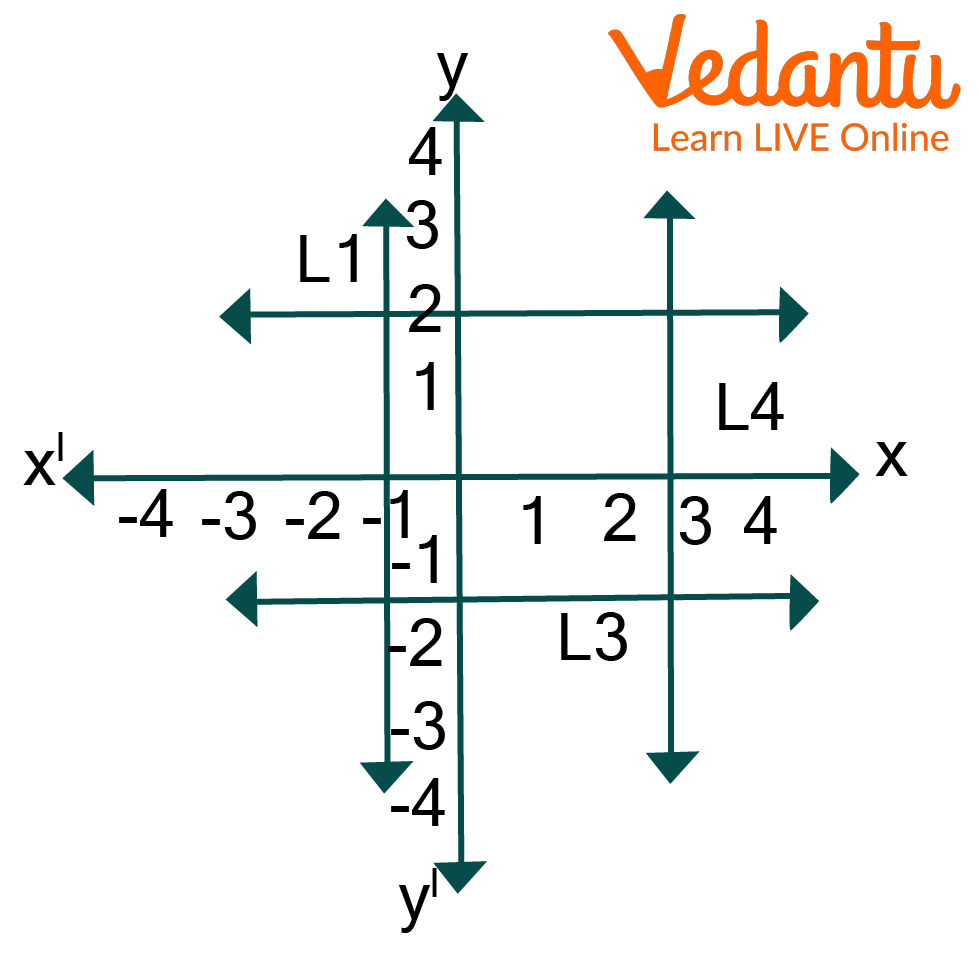
Graphical Representation
Ans: The equation of L1 according to the graph will be Y=2 and for L3 will be Y= -1.5 as the line is placed between -1 and -2
Example 2: Solve the equation of a line 7x – 12 = 16
Ans:
7x -12 = 16
7x = 16 + 12
x = $\dfrac{28}{7}$
x = 4
Example 3: Graphically represent the line of equation Y=5 and also tell the quadrants in which the line lies.
Ans: The line will be parallel to the x-axis and lies in the 1st and 2nd quadrants with all y coordinates with positive values.
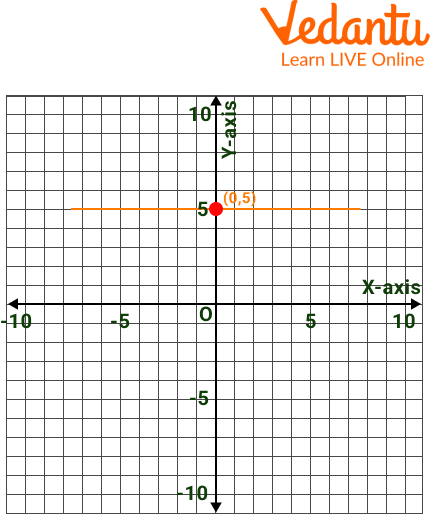
Line of Equation Y=5
Example 4: Which of the following is the equation representing a line parallel to the x-axis?
x=7, y= -2, x=2, y= 6
Ans: A line parallel to the x-axis should be placed on only y coordinates, and the slope of the line parallel to the x-axis is zero and is of the form y=a, which means that the above equations a and c do not satisfy any of the conditions as they will be placed at a point on the x-axis. At the same time, the other two equations represent the equation for a line parallel to the x-axis. Therefore, equation b Y=-2 will be placed at coordinate (0,-2), which will be a parallel line to the x-axis, and equation d Y=6 will also be placed at coordinate (0,6) parallel to the x-axis.
Practice Questions
Q 1: Which quadrant do y=-3 lie in?
Ans: The line will parallel the x-axis and lie in the 3rd and 4th quadrants.
Q 2: Which of the following equations is/are parallel to the x-axis?
6-3y=3
13x-6=20
12y+10=7×10
Ans: Equations 1 and 3 are the equations representing lines parallel to the x-axis.
Q 3: Find the equation for the line perpendicular to the x-axis and 7 units below the x-axis.
Ans: The line will be placed at (0,-7) and in the negative quadrant.
Summary
To conclude all the learnings from that article we can summarise that any line that is parallel to the x-axis on a graph always has the x coordinate as zero, whereas the y coordinate always has a value whether it be negative or positive. Moreover, in this article, we also saw various solved examples and practice questions. Lines parallel to the x-axis. Also, we saw how to solve and represent them over graphs. With this, we would like to end this article and hope that we were easy and clear to understand.
FAQs on Which Graph is Parallel to the X-Axis?
1. What is the slope? What is the slope of the line parallel to the x-axis?
Slope is defined as the change in the value of the y-axis divided by the change in the value of the x-axis of a line. The slope of the line parallel to the x-axis is zero.
2. Why are graphs important or why do we make use of graphical representations?
Graphs are usually used by people to represent large quantities easily in just one pictorial representation. Compare the number of things, numbers, etc. Graphs are easier to use because. They are easy to understand and read. There can be various kinds of graphs. For example, line graphs, pie charts, etc.
3. When is a line parallel to the y-axis?
x = k is the equation of the line perpendicular to the y-axis where "k" represents a constant. The above equation is the simplified version of a line equation perpendicular to the y-axis. The distance from the y-axis to the line x=k is also known as "k” units.
