




Step-by-Step Subtraction Techniques for Young Learners
As we all know, subtraction is a mathematical operation that takes part away from another value. Here in this lesson, we will understand subtraction, types of subtraction models, subtraction by crossing out, and some solved examples on add and subtract for class 2. Subtraction is the series of taking away a number from another. It is a primary operation denoted by a subtraction symbol (-) and is the method of calculating the difference between two numbers. So, let’s further learn about it in this article by understanding more about it and solving some questions.
What is Subtraction?
Subtraction is used to find the difference between numbers. When we have a group of objects, and you take away a few objects, the group becomes smaller. Subtraction methods are many ways numbers can be subtracted. The method will depend on the problem. We will be going to study in the future.
E.g. you bought 10 balls for your friend, and your friend takes 7 balls. This can be written as 10-7=3 and is read as “ ten minus seven equals three.” Here, we performed the subtraction operation on two numbers 10 and 7 to get the difference of 3.

Subtraction
Types of Subtraction Models
Teaching all four models of subtraction-take-away, comparison, completion and whole/part/part--can better train elementary school children to think abstractly and relate their math knowledge to the real world.
Take-Away Model
The takeaway model is the most commonly taught subtraction model. It teaches children that taking away some objects from a set results in fewer objects in the set. To teach children the take-away model, set a particular number (e.g. 8) of objects (apples, oranges, blocks, etc.) in front of them and ask them to take away a small number (e.g. 3) of objects. Then ask them how many objects remain. In some exercises, children learn that subtracting objects from a set results in a smaller number (e.g. 8 -3 = 5 ).
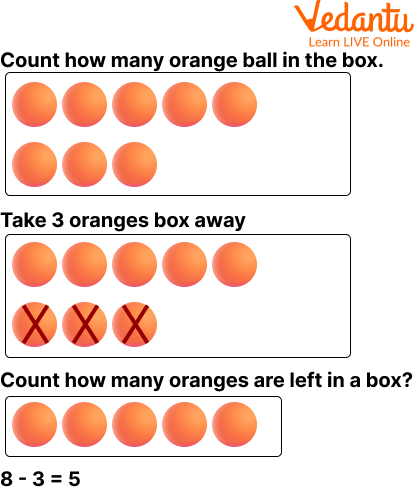
Take away model
Completion Subtraction
The completion subtraction model makes children understand algebra lessons since it forces children to manipulate variables in a basic subtraction equation. For example, a completion subtraction is “7 +? = 10.” Use the same blocks or orange balls you used in the takeaway model to teach children this concept. So here, if 3 balls are added to the 7 orange balls, then it will become 10.
So to get this three, we need to do the subtraction, i.e. 10 - 7 = 3.
Comparison Model
The comparison model of subtraction, which involves comparing two different numbers, is a little more challenging to visualise than the takeaway model. An example of comparison subtraction is “If Ram is 26 and Shyam is 36, how many years older is Shyan than Ram?” Since by using these types of problems, children understand concepts easily.
Whole/Part Model
The part model of subtraction involves categories of objects that need to be subcategorised: “I have five mangoes for sale. Three are green mangoes. How many aren’t green apples?”. In this way, we can categorise the objects and use this model.
How to Solve Subtraction by Crossing Out?
Crossing out is a memory game that models subtraction situations in a frame using crossing out (strike-through) and the matching equation without the difference. Subtract models subtraction situations in a frame using crossing out (strike-through) and the matching difference.

Subtraction by Crossing Out
Solved Examples on Add and Subtract for Class 2
Q.1. Find out the number of apples in the box. If the box contains 10 apples and 6 are removed, how many apples are left in the box?
Solution: Total number of apples in the box is 10.
Out of which, 6 apples are removed.
The number of apples left is given by,
10 -6 =4
Thus the number of apples left in the box is 4.
Q2. Newton catches 25 fish in a lake. He puts 13 fish back. How many fishes does he have now?
Solution: No. of fish caught are 25 fish.
No. of fish that were put back are 13 fish.
Fishes left are given by,
25 - 13 =12.
Thus the number of fish left is 12.
Q3. There are 39 birds in a tree. A loud noise scares 16 birds away, what number of birds are left in the tree?
Solution: There are 39 birds in a tree.
Out of which, 16 birds away from a tree.
Left birds are given by,
39 - 16 =23.
Thus the number of birds left in the tree is 23.
Practice Questions
Q.1. Mark had 10 blue marbles. Jim had 6 red marbles. What number of marbles do they have in total?
Ans: 16.
Q.2. There are 6 blue Marlins and 2 snappers in the pond. How many fish are there in total?
Ans: 4.
Q.3. Mary picked 11 cherries off the tree. Her brother Bill picked 8. How many cherries are left?
Ans: 3.
Summary
In this chapter, we have learned that subtraction is a mathematical operation that takes part away from another value. We also learnt about subtraction, types of subtraction methods, and how to solve subtraction by crossing out. When solving subtraction problems, the 1-digit number can be subtracted more easily, but for larger numbers, we need to split the numbers into columns using their respective values. By solving subtraction questions, we develop an understanding of methods and their applications, which will help us solve such difficult questions.
FAQs on Subtraction Strategies for Grade 2
1. What are subtraction strategies for Grade 2 students?
Grade 2 students can use several subtraction strategies, such as
- counting back
- using number lines
- breaking apart numbers
- subtracting in parts
2. Why are number lines useful in learning subtraction?
A number line helps Grade 2 students see subtraction as movement backward. By jumping to the left, children can count down and easily find the difference between numbers, making subtraction more visual and easier to understand at this math level.
3. How does breaking apart numbers help with subtraction?
Breaking apart numbers, also known as decomposing, encourages students to split a large number into smaller, easier chunks. For example, for $15-7$, they might subtract $5$ to get $10$, then subtract $2$ more, making the math much simpler.
4. What is the counting back strategy in subtraction?
The counting back strategy means starting at the largest number and counting backward for the amount being subtracted. For $12-4$, count back four numbers from $12$. This method reinforces how subtraction takes away quantity in steps.
5. Can subtraction be shown using objects or pictures?
Yes, using objects or drawings helps Grade 2 students see what subtraction means.
- Take away counters
- Cross out items
- Draw pictures
6. How can we subtract by making ten in Grade 2?
The make ten strategy involves breaking numbers apart to form $10$ first. For example, to solve $13-4$, break $4$ into $3$ and $1$, subtract $3$ to make $10$, then take away $1$ for the answer, $9$.
7. What mental math strategies help with subtraction in Grade 2?
Grade 2 students can use mental math strategies like:
- Using doubles facts
- Counting back in steps
- Breaking apart numbers
- Making ten
8. Why should students learn different subtraction strategies?
Learning various subtraction strategies helps Grade 2 students solve problems in multiple ways. This flexibility builds a deeper understanding of subtraction, supports problem-solving, and prepares students for more advanced math topics in later grades.
9. How does using fact families support subtraction learning?
Working with fact families shows the relationship between addition and subtraction. For example, knowing $8+5=13$ helps students see that $13-8=5$. This connection makes subtraction facts easier to remember and use quickly.
10. What is the purpose of estimating in subtraction?
Estimation in subtraction helps Grade 2 students quickly judge if an answer is reasonable. By rounding numbers and finding close answers, children gain confidence in their subtraction work and develop important number sense skills.
11. Can you explain the concept of subtracting in parts?
Subtracting in parts, or partial differences, means breaking the problem into smaller subtraction steps. For $34-12$, first subtract $10$ to get $24$, then subtract $2$ more to reach $22$. This strategy helps manage larger numbers more easily.

















