




How to Identify and Use Square Numbers in Real Life
In Mathematics, a square number or "perfect square" is nothing but an integer that's the square of an integer; in other words, it's the product of some number with itself. For example, when we multiply $2 × 2 = 2^2$, we get 4. Here,4 is a square number. Square numbers are always positive, they cannot be negative because when a negative number is multiplied by the same negative number, it results in a positive number. For example, $(-6)^2 = -6× -6 = 36$ (two negative signs multiplied by each other result in a positive sign). When we multiply -6 by -6, the result is 36 and it is a positive square number.
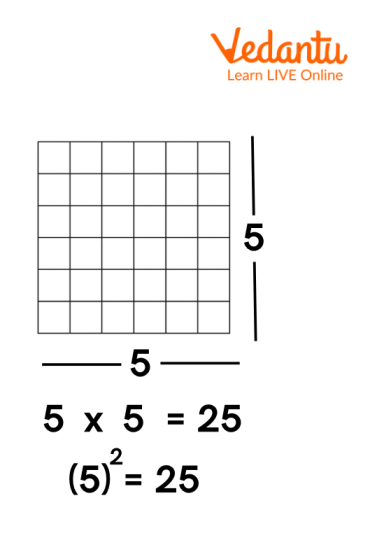
Square Numbers
Square Number Pattern
When we multiply an integer (a “whole” number, positive, negative, or zero) by itself, the approaching resulting product is called a square number, or an ideal square or simply we can say “a square.” So, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, and so on, are all square numbers. This is known as the square number pattern.
Pattern with Square Numbers
When you multiply a number by itself, you get a square number. The series of numbers, which are perfect squares, are represented by the square number pattern. A sequence of numbers that forms a square-shaped pattern is referred to as Patterns with Squares sequence.
Math Patterns between Square Numbers
Difference between Square Numbers
The difference between two consecutive squares is usually an odd number. If n is any number, then the difference between the square of n and the square of the next natural number (n + 1) is 2n + 1.
Adding Odd Numbers
If a number is a square number, it is the sum of consecutive or successive odd numbers beginning with 1. Consider the following:
1 (first odd number) \[ = {\rm{ }}1{\rm{ }} = {\rm{ }}1^2\]
\[1{\rm{ }} + {\rm{ }}3{\rm{ }}\] (sum of first two odd numbers) \[ = {\rm{ }}4{\rm{ }} = {\rm{ }}2^2\]
\[1{\rm{ }} + {\rm{ }}3{\rm{ }} + {\rm{ }}5{\rm{ }}\] (sum of first three odd numbers) \[ = {\rm{ }}9{\rm{ }} = {\rm{ }}3^2\]
\[1{\rm{ }} + {\rm{ }}3{\rm{ }} + {\rm{ }}5{\rm{ }} + {\rm{ }}7{\rm{ }}\] (sum of first four odd numbers) \[ = {\rm{ }}16{\rm{ }} = {\rm{ }}4^2\]
\[1{\rm{ }} + {\rm{ }}3{\rm{ }} + {\rm{ }}5{\rm{ }} + {\rm{ }}7{\rm{ }} + {\rm{ }}9\] (sum of first five odd numbers) \[ = {\rm{ }}25{\rm{ }} = {\rm{ }}5^2\]
A number that is not a perfect square cannot be put in this form. Also, we will check if a number is a perfect square or not. Allow us to now consider the number 16. Subtracting 16 from the series of successive odd numbers and getting 0, as a result, will tell us that 16 may be a perfect square.
\[16{\rm{ }}-{\rm{ }}1\;\;\; = {\rm{ }}15\]
\[15{\rm{ }} - {\rm{ }}3\;\;\; = {\rm{ }}12\]
\[12{\rm{ }} - {\rm{ }}5\;\;\; = {\rm{ }}7\]
\[7{\rm{ }} - {\rm{ }}7\;\;\;\;\; = {\rm{ }}0\]
This means that 16 is a perfect square. Any non-perfect square will leave a remainder aside from zero. Try the successive subtraction by consecutive odd numbers for 35.
Sum of Consecutive Natural Numbers
Any odd square number is often expressed as the sum of two consecutive natural numbers. Lets take any odd perfect square say \[441,{\rm{ }}21^2{\rm{ }} = {\rm{ }}441{\rm{ }} = {\rm{ }}220{\rm{ }} + {\rm{ }}221\]. Similarly, we've \[23^2{\rm{ }} = {\rm{ }}529{\rm{ }} = {\rm{ }}264{\rm{ }} + {\rm{ }}265\]and so on.
Product of Two Consecutive Even Or Odd Natural Numbers
Consider the merchandise of two consecutive even numbers. For Example, \[20{\rm{ }} \times {\rm{ }}22{\rm{ }} = {\rm{ }}\left( {21{\rm{ }}-{\rm{ }}1} \right){\rm{ }} \times {\rm{ }}\left( {21{\rm{ }} + {\rm{ }}1} \right){\rm{ }} = {\rm{ }}21^2{\rm{ }}-{\rm{ }}1.\;\]the merchandise of two consecutive odd numbers, \[21{\rm{ }} \times {\rm{ }}23{\rm{ }} = {\rm{ }}\left( {22{\rm{ }}-{\rm{ }}1} \right){\rm{ }} \times {\rm{ }}\left( {22{\rm{ }} + {\rm{ }}1} \right){\rm{ }} = {\rm{ }}22^2{\rm{ }}-{\rm{ }}1\]. produce an identity
\[\left( {a{\rm{ }} + {\rm{ }}1} \right){\rm{ }}\left( {a{\rm{ }}-{\rm{ }}1} \right){\rm{ }} = {\rm{ }}a^2{\rm{ }}-{\rm{ }}1.\]
Solved Questions
Problem 1: Check if 121 may be a perfect square by the method of the sum of successive odd numbers from the Maths patterns.
Solution: Subtracting the amount by a series of successive odd numbers will give
\[\begin{array}{*{20}{l}}{121{\rm{ }}-{\rm{ }}1 = {\rm{ }}120}\\{120{\rm{ }}-{\rm{ }}3 = {\rm{ }}117}\\{117{\rm{ }}-{\rm{ }}5 = {\rm{ }}112}\\{112{\rm{ }}-{\rm{ }}7 = {\rm{ }}105}\\{105{\rm{ }}-{\rm{ }}9 = {\rm{ }}96}\\{96{\rm{ }}-{\rm{ }}11\; = {\rm{ }}85}\\{85{\rm{ }}-{\rm{ }}13\; = {\rm{ }}72}\\{72{\rm{ }}-{\rm{ }}15\; = {\rm{ }}57}\\{57{\rm{ }}-{\rm{ }}17\; = {\rm{ }}40}\\{40{\rm{ }}-{\rm{ }}19\; = {\rm{ }}21}\\{21{\rm{ }}-{\rm{ }}21\; = {\rm{ }}0}\\\;\end{array}\]
Hence, 121 is a perfect square.
Problem 2: Express 3721 as the sum of consecutive natural numbers.
Solution: We all know $61^2$ = 3721. Taking the half 3721, we can have an estimation for the choice of the consecutive natural numbers. So, 3721 is often expressed as the sum of 1860 and 1861, i.e., \[3721{\rm{ }} = {\rm{ }}1860{\rm{ }} + {\rm{ }}1861.\]
Problem 3: Find the number that has 1 zero at the end, and the square of that number will produce another zero at the end.
24
656
458
10,20
Solution: the right option is D. for instance,
\[10{\rm{ }} \times {\rm{ }}10{\rm{ }} = {\rm{ }}100\]
\[ \bullet \;20{\rm{ }} \times {\rm{ }}20{\rm{ }} = {\rm{ }}400\]
Therefore D is the correct option for the problem.
Summary
In this article, we learned what a square is and what a square pattern is. We have also learned to calculate squares. To explain it, we have also provided solved examples. Children can apply what they learned by practising worksheets related to patterns and squares.
FAQs on Square Numbers For Kids: Definition, Examples & Tips
1. Is 1 a Square Number?
Ans: Yes. When you multiply a number by itself, you will get the product as a Square number. Hence, if we multiply 1 by itself, we get 1, i.e., 1 x 1 = 1.
1 is called a square number because it gives the area of a square with side length as an integer. We can express it as $a x a = a^2$ i.e 1 x 1 = 12 = 1.
2. What is a Perfect Square?
Ans: A number's square can be calculated by multiplying it by itself. A number that can be written as the product of two equal integers is called a perfect square. 100 is a perfect square, for example, because it is the product of two equal integers, 10 x 10 = 100.
3. What are some properties of Perfect Squares?
Ans: Following are a few properties of Perfect Squares:
Numbers that end with 2, 3, 7, or 8 are never perfect squares, while numbers that end in 1, 4, 5, 6, 9, or 0 are perfect squares.
A perfect square is never a number that ends with an odd number of zeros.
An even number's square is always even, whereas an odd number's square is always odd.











