Reflection in x-axis

Have you ever thought about how you would represent the reflection of a point about the x-axis? This is done using the concept of reflection of a point in the x-axis. If you do not know about it, do not get worried, as this article covers all the concepts of reflection in the x-axis and the rules to find the reflection using attractive images so that the children can easily grasp the topics. Let us begin with our learning.

What is the Reflection of a Point in the x-axis?

Reflection of a point in the x-axis states that when a point is reflected across the x-axis, the x-coordinate remains constant, while the y-coordinate is assumed to be the additive inverse of the given ordinate. For example, a point (x, y) is reflected across the x-axis as (x, -y).

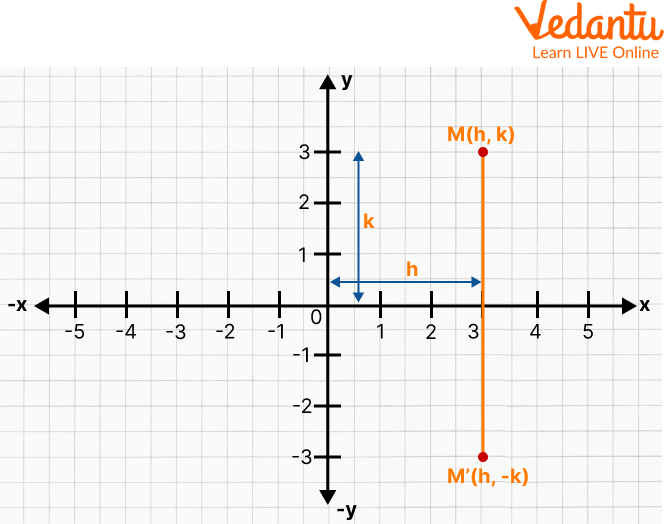
Reflection of a Point About the x-axis

A Point on the x-axis has Coordinates

A point on the x-axis has coordinates in the form of ordered pairs having the form (h, 0), where h is the point on the x-axis. When y = 0, the value of the x-coordinate or abscissa can be anything, irrespective of the value of the ordinate.

Rules to Find the Reflection in the x-axis

There is no hard rule to find the reflection in the x-axis; you just need to do is, to follow these two simple steps, which are given below:

1. Keep the coordinates of the x-axis fixed

2. Reverse the sign of the y-coordinate

The obtained value of the x-coordinate and y-coordinate is the reflection of a point about the x-axis.

Solved Examples

Q 1. Find the reflection of a point about the x-axis of the following:

1. (-1, 6)

2. (2, 1)

Ans: For part 1, we need to follow the given steps:

1. Read the coordinates (-1, 6) and find out in which quadrant it lies, i.e. the 2nd quadrant

2. Mark the value of x = -1 and y = 6 in the appropriate quadrants

3. Highlight the point and write its coordinates

4. To find its reflection, keep the abscissa same, i.e. x-coordinate is -1, and take the additive inverse of the ordinate, i.e. -6

5. Now, choose the quadrant for the new coordinates, i.e. (-1, -6)

6. Mark the values of x = -1 and y = -6 in the respective quadrants

7. Highlight the point and write its coordinates

This is how you find the reflection of a point in the x-axis.

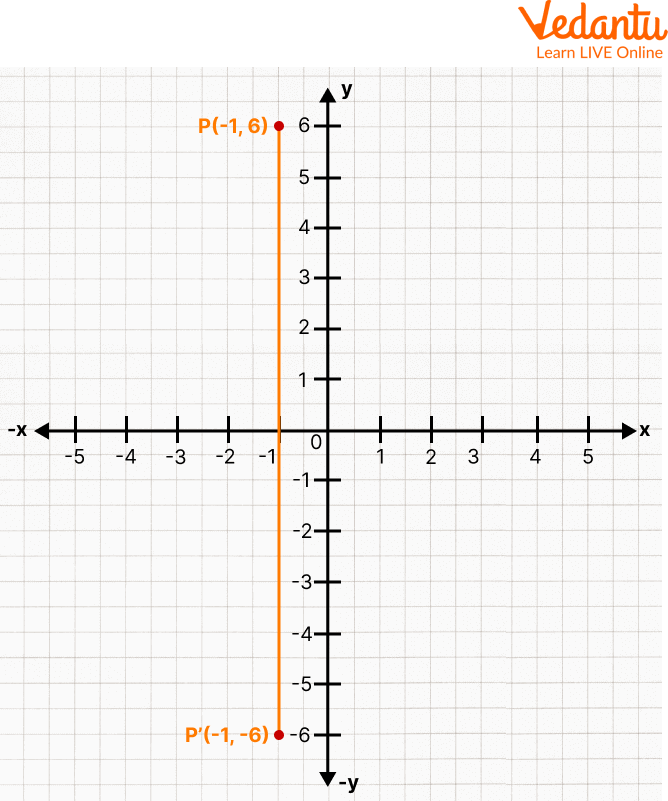
Reflection of a Point About the x-axis

For part 2, we need to follow the given steps:

1. Read the coordinates (2, 1) and find out in which quadrant it lies, i.e. the 1st quadrant

2. Mark the values of x = 2 and y = 1 in the respective quadrants

3. Highlight the point and write its coordinates

4. To find its reflection, keep the abscissa same, i.e. 2 and take the additive inverse of ordinate, i.e. -1

5. Now, choose the quadrant for the new coordinates, i.e. (2, -1)

6. Mark the values of x = 2 and y = -1 in the respective quadrant

7. Highlight the point and write its coordinates

This is how you find the reflection of a point (2,1) on the x-axis.

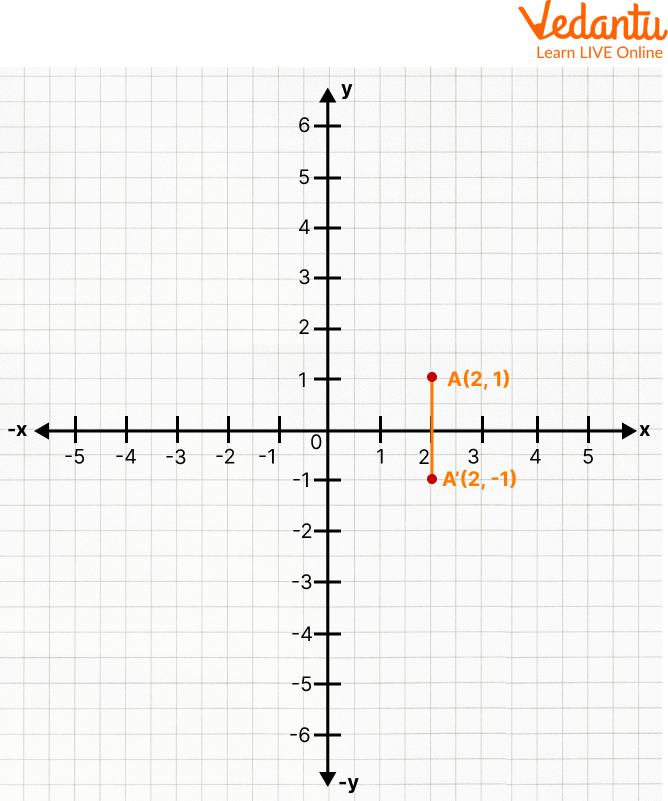
Reflection in the x-axis

Practice Problems

Q 1. Find the reflection about the x-axis of the point (2, 6).

Ans. (2, -6)

Q 2. Find the reflection of a point on the x-axis of the following:

• (-7, -3)

• (3, 1)

Ans. (-7, 3)

• (3, -1)

Q 3. Compute the reflection of a point on the x-axis of the following:

• (4, -5)

• (-8, 2)

Ans. (4, 5)

• (-8, -2)

Summary

Summing up here with the concept of reflection in the x-axis. This article describes all the topics, including rules to find the reflection, the coordinate of a point on the x-axis, etc. Here we have discussed in depth how to solve the problems based on the reflection of a point in the x-axis. Some practice problems are also assigned to the students along with their answers so they can practice more and gain proficiency in the concept. Hoping you enjoyed reading the article.