Recurring Numbers

The numbers which tend to repeat after a decimal point infinitely in a uniform manner are known as recurring numbers, also known as recurring or repeating decimal numbers. After a decimal point, two types of numbers are found, recurring and non-recurring. Some recurring numbers examples are -

\[\frac{1}{6} = 0.1666666.....\] Here 6 repeats forever,

\[\frac{{10}}{3} = 3.3333333.....\] Here 3 repeats forever,

\[\frac{1}{7} = 0.142857142857142857\] Here 142857 repeats forever, etc.

What are Recurring Numbers?

Recurring numbers or repeating decimal numbers are those numbers whose digits repeat their values uniformly and infinitely after a decimal point, and the repeated digit or set of digits is never zero. The repeated numbers are fixed and they repeat in a continuous manner. Since it is one of the types of decimal numbers, there are other types of decimal numbers too.

Normally, decimal numbers can be divided into two categories:

• Recurring decimal number– Numbers whose digits repeat infinitely.

• Non-recurring decimal number– Numbers whose digit does not repeat.

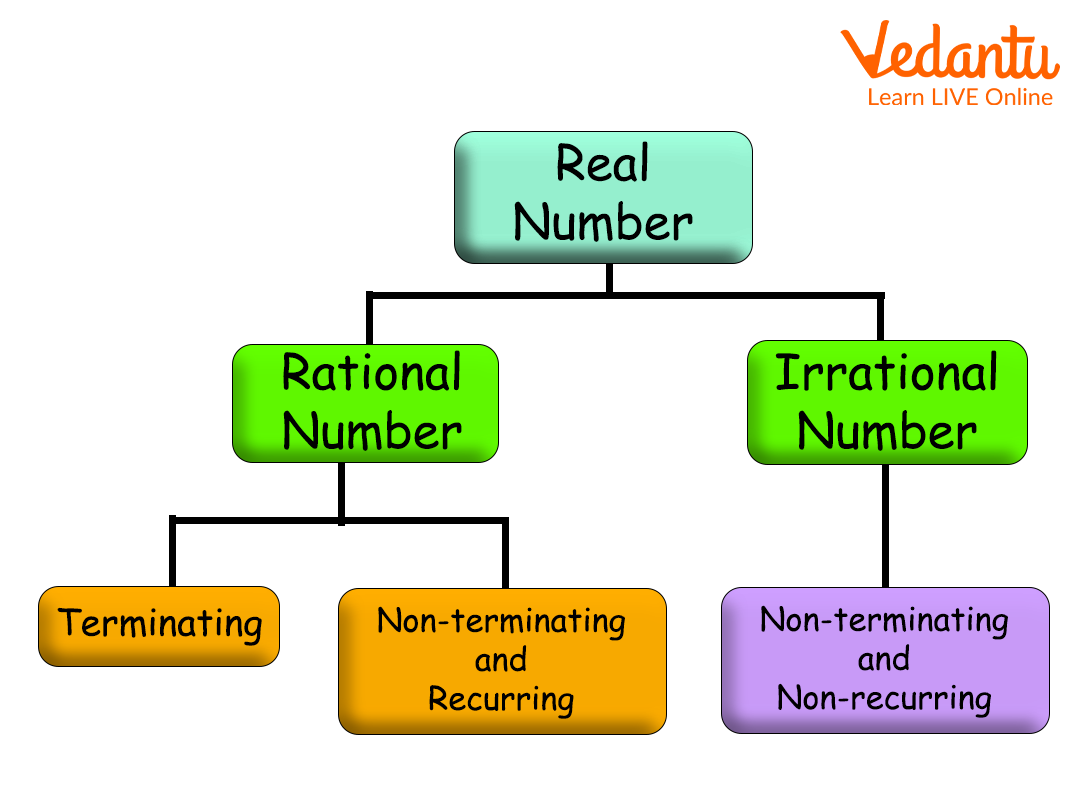
Types of Real Numbers

Representation of Recurring Numbers

Recurring numbers are represented by putting bars above the repeating digit. Instead of a dash we can also put a dot on the top of the repeating digit.

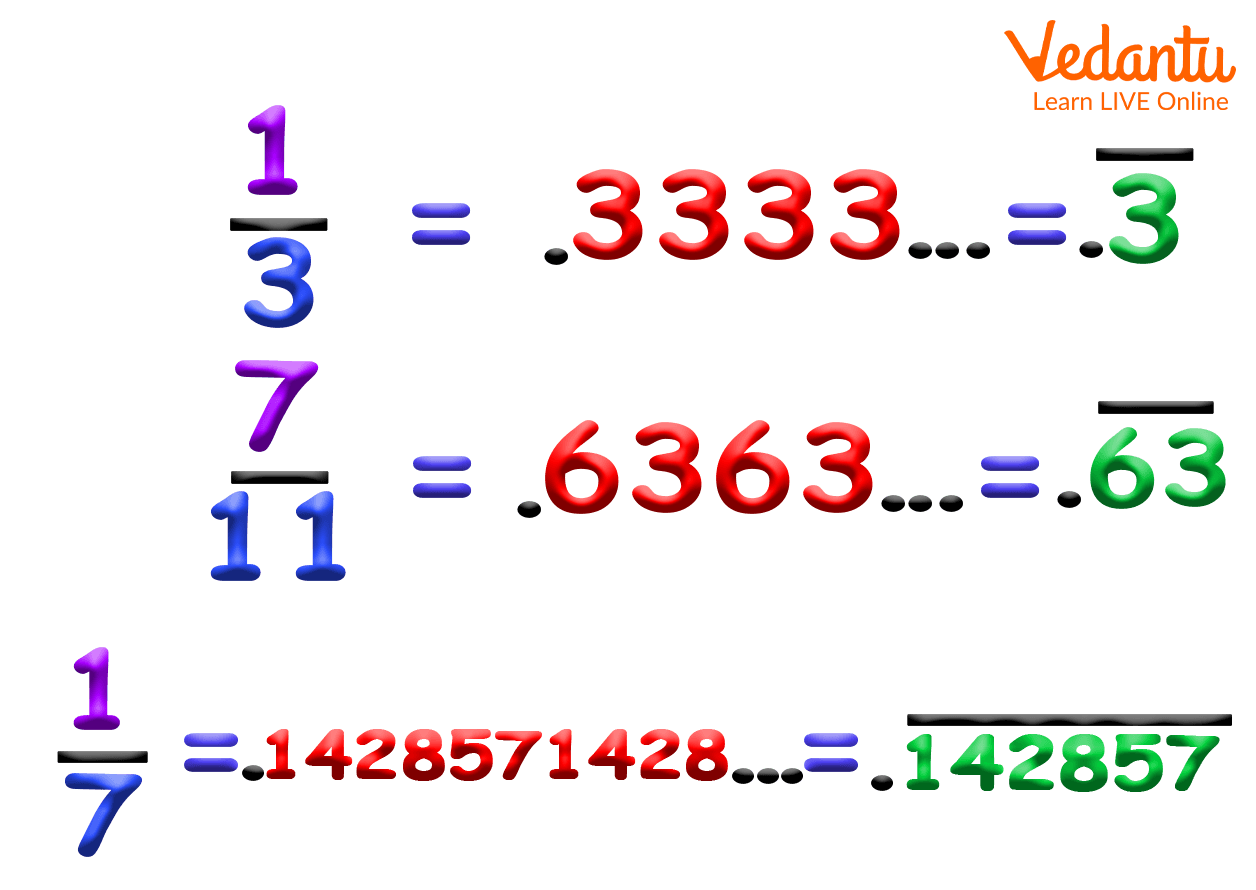
Conversion of Recurring Numbers

Conversion of Recurring Numbers to Fractions

In recurring numbers, the decimal digits are repeated. Let’s discuss some points for the conversion of recurring decimal into fraction.

• Let us consider a number X, which is a recurring decimal.

• Then count the number of recurring digits. Name them y.

• Now, recurring decimals are multiplied by powers of 10 according to decimal number.

• To eliminate the recurring number, we have to subtract the answer of point 1 from point 3.

• Now, after solving the expression, we will get the value of X.

• Expresses the value of X as a fraction.

Let’s understand this with the help of recurring numbers examples.

Let the value of X be equal to 0.989898

from the value of X we clearly see that two digits are repeating.

so the number of recurring digits is 2.

Multiply 10 to power 2 which is equal to 100.

Now \[100{\rm{X = 98}}{\rm{.98989898}}\]

After subtracting the value of x from the above equation, we get \[99{\rm{X = 98}}\]

After solving this, we get the value of X, which is equal to,

,\[{\rm{X}} = \frac{{98}}{{99}}\]

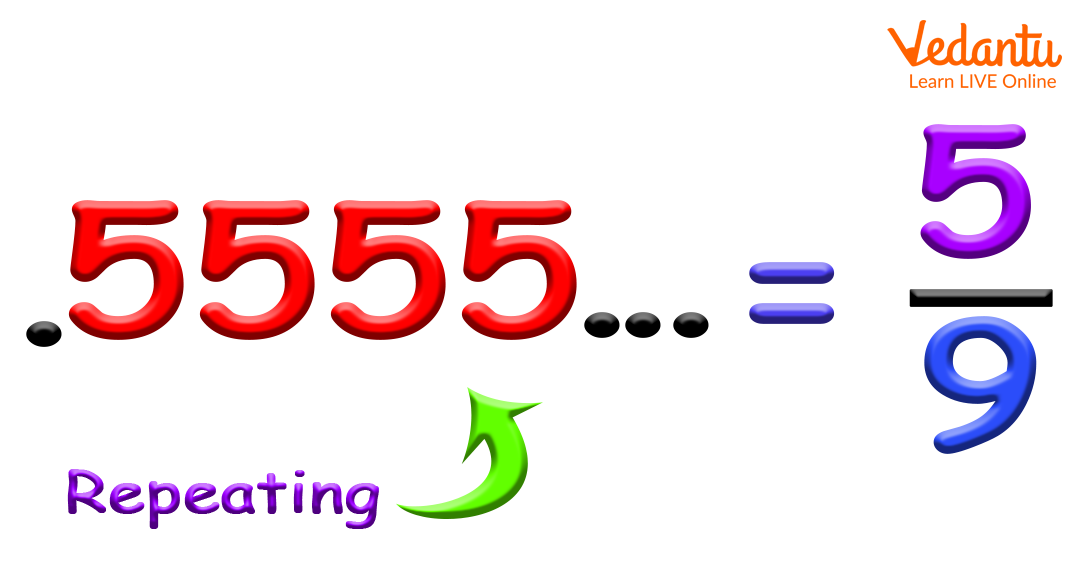
Conversion of Recurring Numbers to Fractions

Are Recurring Numbers Rational Numbers?

We know that rational numbers are the ratio of two integers where the denominator is not equal to 0. Representation of rational numbers is \[\frac{{\rm{p}}}{{\rm{q}}}\] where p and q are integers and q is not equal to 0. So we know that in maths there are several ways to represent a number.

Let's take an example. \[\frac{1}{3} = 0.33....\] where \[\frac{1}{3}\] is a rational number and 0.333… is a recurring number. Actually recurring numbers are rational numbers because these numbers have repeating digits after decimal.

Non Terminating and Non Recurring Numbers

All irrational numbers are non-terminating and non-recurring decimal numbers. Root numbers cannot be expressed in the form of fractions because the value of the decimal in the recurring number can go up to infinity so for solving this we have to do complicated calculations. Because these numbers are non-terminating and non-repeating decimals,example 1.414211356… This is the value of under root two, which is non- terminating and non-repeating.

Solved Examples

1. Find the fraction form of 1.555….

Ans: Let us consider the number x.

Where x is equal to 1.555….

\[{\rm{x}} = 1.555.....\].————(1)

Now in this number only one digit is repeating, that is 5.

So we multiply x by 10

\[10{\rm{x}} = 15.55\]————(2)

Subtract equation (1) from equation (2)

\[10{\rm{x}} - {\rm{x}} = 15.55 - 1.55\]

\[9{\rm{x}} = 14\]

\[{\rm{x}} = \frac{14}{9}\]

So here we convert given recurring number into rational number

2. Find the fraction form of 15.34545….

Ans: Let us consider the number x.

Where x is equal to 15.34545…

\[{\rm{x}} = 15.34545\]

x=15.34545————(1)

Here two digits are repeating, that is 45.

Now multiply the equation by 1000.

\[1000{\rm{x}} = 15345.4545.....\]————(2)

Now we have to keep the same repeating digit on the right side of the decimal, so multiply equation (1) by 10

\[10{\rm{x}} = 153.4545.....\]————(3)

Subtracting equation(3) from equation (2)

\[990{\rm{x}} =15192\]

\[{\rm{x}} =\frac{{15192}}{{990}}\]

\[{\rm{x}} = \frac{{844}}{{55}}\]

Conclusion

So, in this article we learned about recurring numbers and how they are represented, how recurring numbers are converted into rational numbers. We also learned some interesting facts about rational numbers and solved non terminating recurring numbers examples. Afterwards, we can solve problems of recurring numbers.