What Is Ratio And Proportion In Year 6 With Formulas And Solved Examples
One of the problems that people face on a daily basis is the problem of comparison. So, the material comparison is important for learning. When comparing two quantities of the same kind, the ratio is used. According to the ratio formula for two numbers, a and b are equal to a : b or a/b. Two or more of such ratios are said to be in proportion when they are equal.
The basic concepts of ratio and proportion are ratios and fractions. The concept of ratio and proportion are the foundations for many other mathematical topics. They have applications in our daily lives while comparing heights, weights, distances, or time, or when dealing with business transactions, or when adding ingredients to a recipe, ratio and proportion will help us. In this article, we are going to discuss the concept of ratio and proportion in Year 6.
What is Ratio?
In some situations, comparing two quantities using the division method is very efficient. A ratio can be defined as the comparison or simplified form of two quantities of the same kind. This relation shows us how many times one quantity equals another. To put it another way, a ratio is a number that can be used to express one quantity as a fraction of the other.
It's called a ratio when we divide two quantities to compare them. The ratio is denoted by the sign ":".
Formula for Ratio
If we have two quantities and we need to find the ratio between them, the ratio formula is as follows:
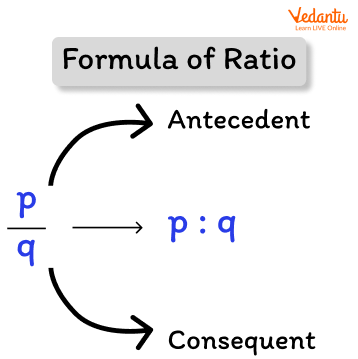
Formula of ratio
Here, a and b can be any two quantities.
Points to Remember
The fraction a/b is the ratio of two non-zero numbers a and b, and it is written as a:b, or 'a to b.' 3/4 represents the ratio 3:4, where 3 is the antecedent and 4 is the consequent. We name a as the first term or antecedent and b as the second term or consequent in the ratio a : b.
What are equivalent ratios? We get a ratio equivalent to the given ratio by multiplying or dividing each term of a ratio by the same non-zero number. As a result, multiplying and dividing each term of the ratio by the same number (non-zero) has no influence on the ratio.
What is Meant by Proportion?
Proportion is a part, share, or number is considered in relation to a whole, most commonly in a comparative relation. The proportion of two equivalent ratios is always the same. It is an equation or statement that shows the equality of two ratios or fractions. It's a comparison of two numbers in Mathematics. So, if two sets of given numbers increase or decrease in the same ratio, the ratios are said to be directly proportional to each other. The signs (: :) or equal to (=) is used to represent proportions.
Formula for Proportion
Let’s assume that the two ratios are p:q and r:s are in proportion. The two terms ‘q’ and ‘r’ are called ‘mean terms,’ and the terms ‘p’ and ‘s’ are known as ‘extreme terms.’
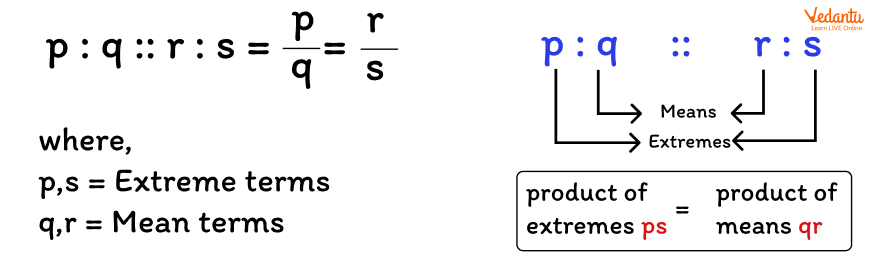
Mean terms and extreme terms in proportion
Ratio and proportions are considered to be two sides of the same coin. When the values of two ratios are equal, they are said to be in proportion. To put it another way, it compares two ratios.
The proportion can be classified into the following categories, such as:
Direct Proportion: It shows the direct relationship between two quantities, in which if one increases, the other increases as well, and vice versa.
Inverse Proportion: It describes the indirect relationship between two quantities in which one increases while the other decreases and vice versa.
Continued Proportion: Any three quantities are said to be in a continued proportion if the ratio between the first and the second is equal to the ratio between the second and the third.
Tips and Tricks
The only thing that can be compared are two quantities with the same units.
Only if the two ratios are equal are they said to be in proportion.
We can also use the cross-product method to see whether two ratios are equal and form a proportion.
Examples
1. Are the ratios 2:4 and 5:10 said to be in proportion?
Sol: 2:4= 1/2 = 0.5 and 5:10= 5/10= 0.5
Since both the ratios are equal, they are said to be in proportion.
2. What is the value of x in 10 : x :: 4 : 5?
Sol: Using the proportion formula,
⇒ a : b :: c : d = a/b = c/d
⇒ 10/x = 4/5
⇒ x = 12.5
So, the value of x = 12.5
Conclusion
Many activities, such as cooking, using maps, and reading scale drawings, depend on the concept of ratio and proportion. Fractions are used to describe a lot of things, like ratio and proportion. A ratio is when a fraction is written in the form a:b, whereas a proportion states that two ratios are equal. In this example, a and b can be any two integers. The concepts of ratio and proportion Year 6 are the foundation for understanding various concepts in mathematics and science.
FAQs on Ratio And Proportion For Year 6 Complete Guide
1. What is ratio and proportion in Year 6 Maths?
A ratio compares two quantities, while a proportion shows that two ratios are equal. In Year 6 Maths, pupils learn to:
- Write ratios using the : symbol (e.g., 2:3)
- Simplify ratios to their smallest form
- Solve proportion problems where two ratios are equal
2. How do you write a ratio?
A ratio is written using the : symbol to compare two quantities in order. For example:
- If there are 3 boys and 5 girls, the ratio of boys to girls is 3:5.
- The order matters, so 3:5 is different from 5:3.
3. How do you simplify a ratio?
To simplify a ratio, divide both parts by their highest common factor (HCF). Follow these steps:
- Find the HCF of both numbers.
- Divide each part by the HCF.
- HCF of 8 and 12 is 4.
- 8 ÷ 4 = 2 and 12 ÷ 4 = 3
- Simplified ratio = 2:3
4. What is the formula for proportion?
A proportion shows two ratios are equal and can be written as a/b = c/d. To check a proportion:
- Multiply across (cross multiply): a × d = b × c
- Is 2/3 = 4/6?
- 2 × 6 = 12 and 3 × 4 = 12
- Since both sides equal 12, it is a proportion.
5. How do you solve ratio problems step by step?
To solve a ratio problem, first find the value of one part, then multiply to find the rest. Steps:
- Add the parts of the ratio.
- Divide the total amount by the total parts.
- Multiply by each ratio number.
- Total parts = 1 + 3 = 4
- £20 ÷ 4 = £5 per part
- Amounts are £5 and £15
6. What is the difference between ratio and fraction?
A fraction compares a part to the whole, while a ratio can compare part-to-part or part-to-whole. For example:
- If 2 out of 5 students wear glasses, the fraction is 2/5.
- The ratio of glasses to no glasses is 2:3.
7. Can you give an example of a proportion problem?
A proportion problem shows two equivalent ratios, such as scaling amounts up or down. Example:
- 3 apples cost £6.
- How much do 6 apples cost?
- Cost = £12
8. How do you find equivalent ratios?
Equivalent ratios are found by multiplying or dividing both parts by the same number. Example:
- Start with 2:5
- Multiply both numbers by 2 → 4:10
- Multiply both numbers by 3 → 6:15
9. Where is ratio used in real life?
Ratios are used in real life to compare quantities and scale amounts. Common examples include:
- Recipes (e.g., 1:2 ratio of sugar to flour)
- Maps and scale drawings
- Mixing paint colours
- Speed (distance to time ratio)
10. What are common mistakes in Year 6 ratio and proportion?
Common mistakes in ratio and proportion include mixing up order and not simplifying correctly. Watch out for:
- Reversing the ratio order (e.g., writing 3:5 instead of 5:3)
- Not dividing both parts when simplifying
- Forgetting to use cross multiplication in proportions
- Adding instead of multiplying when scaling
