




What Are the Differences Between a Point, Line, and Plane?
To begin the study of geometry, it is necessary to know the most basic concept of geometry. However, they cannot be defined. Fortunately, we have innate ideas about these concepts.
Surprisingly, there are three undefined terms of geometry. These three things are called undefined terms because in geometry they do not require a formal definition. They serve as the cornerstones for establishing other terms and theorems. These words themselves are so basic that they are considered true without formally defining them.
They are point, line, and plane. These basic geometrical ideas are defined below.
Point, Line, and Plane
The point, line, and plane are basic geometrical ideas and are not defined. They are considered "primitive concepts" and are the basis of Geometry. We will consider space as a set of points and then, we will be able to give an idea of what a point, line, and plane are:
A point is the smallest object in space, it has no dimension (neither length nor width).
Straight is a line that "does not bend". It has one dimension (it has length, but no width).
The surface on which points and lines can be drawn is called a plane. It is two-dimensional (length and width).
Collinear and Non-Collinear Points
Points that are on the same straight line are referred to as collinear points. These kinds of lines have two points in common. They must lie on the same straight line, even if they don't have to be coplanar.
Non-collinear points are three or more points that do not all lie on the same straight line. They are considered non-collinear points if any one of the points among them is not on the same line.
Types of Straight Lines According to the Position Between them
1. Parallel lines are in the same plane and maintain a certain distance from each other, but they never cross or touch at any point.
An example of parallel lines would be train tracks, even though they seem to touch in the distance. It is because of that feeling that the train tracks are getting closer, but it is not true, besides, infinity is not a point, so saying that they touch at infinity is a curious way of saying that they never touch.

Parallel Lines
2. Intersecting lines intersect at a point. When cut, they divide the plane into 4 regions, that is why we say that they form 4 angles. They have one point in common.

Intersecting Lines
3. Perpendicular lines are a particular case of intersecting lines, in addition to intersecting at a point and forming four right angles (angle of 90 degrees).
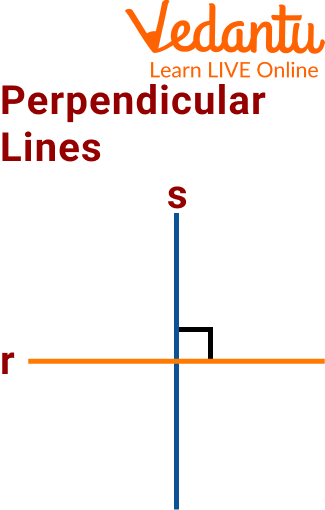
Perpendicular Lines
Solved Examples
Q 1. Find the correct types of lines from the figure given below.
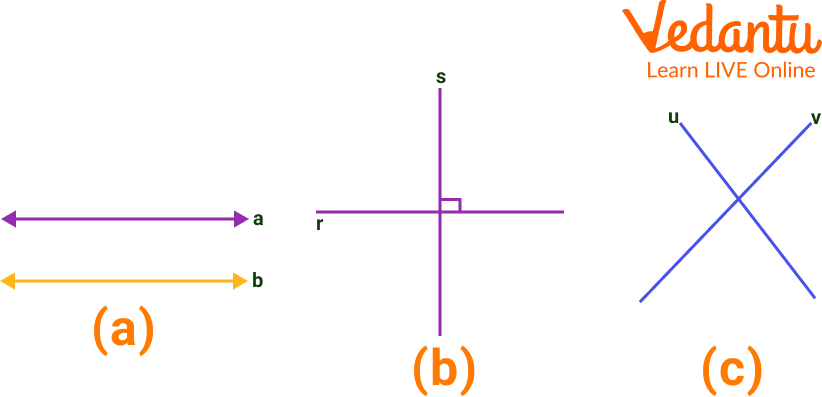
Perpendicular, Parallel and Intersecting Lines
Sol: (a) A pair of parallel lines.
(b) A pair of intersecting or non-parallel lines.
(c) An illustration of perpendicular lines.
Q 2. Identify the collinear points and non-collinear points in the figure given below.
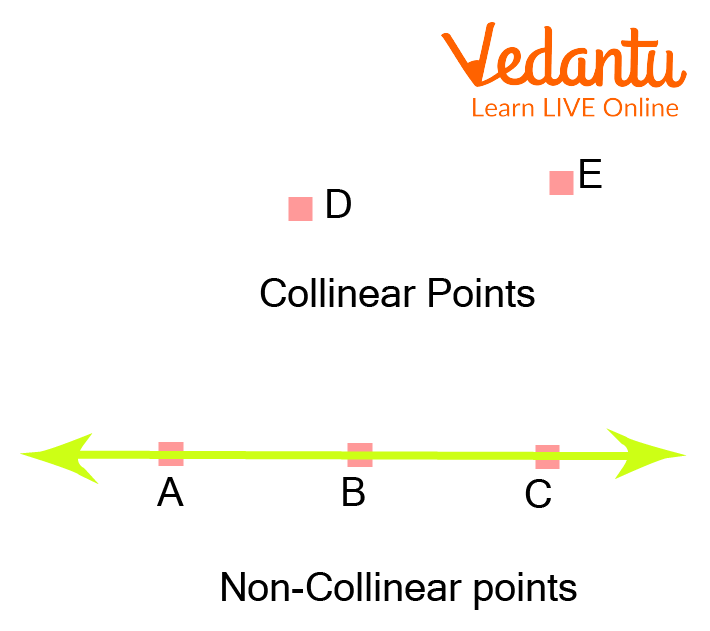
Collinear and Non-collinear Points
Sol: Collinear points are A, B, and C as they all lie on the same straight line. Points D and E are not collinear because they do not lie on the same line.
Q 3. Define parallel lines.
Ans: Parallel lines are coplanar lines. They do not intersect at any point. Although they seem to be intersecting at infinity it is only a curious way to say that they do not intersect at any point.
Q 4. What is a plane in geometry?
Ans: A plane is a flat, two-dimensional surface that consists of all the points that form a straight line by joining each other.
Q 5. Define a straight line and what are coplanar points?
Ans: A straight line is formed by joining two points on a plane, it has length but no width. Coplanar points are the points that lie on the same plane.
Practice Questions
Q 1 Name the undefined terms of geometry.
Ans: Point, Line, Plane
Q 2 Choose the correct statement.
(a) A point has length, breadth, and width
(b) Collinear points do not lie on the same row
(c) A point is represented by a dot.
Ans: (c).
Q 3 Differentiate between parallel lines and intersecting lines.
Ans: Parallel lines do not intersect and intersecting lines intersect at certain points and have one point in common.
Q 4 Why do we say that parallel lines meet at infinity?
Ans: They only seem to meet, in reality, they do not.
Q 5 Define coplanar points and collinear points.
Ans: Coplanar points are those which lie on the same plane whereas collinear points lie on the same line and have two points in common.
Summary
We have learned the three undefined terms of geometry. Undefined terms are those terms that do not require a formal definition. The three terms are point, line, and plane. A point is just a point and is labeled with a capital letter. An endlessly long, straight mark is known as a line and is labeled with two capital letters that represent two points on the line. A plane is a flat surface that never ends in any direction and is labeled with a capital letter along with the word "plane."
FAQs on Point, Line, and Plane Explained: Geometry’s Building Blocks
1. What are the three undefined terms in geometry and what do they represent?
The three fundamental undefined terms in geometry are point, line, and plane. They are considered the building blocks for all other geometric concepts.
- A point represents a specific location in space but has no dimension (no length, width, or height). It is usually denoted by a capital letter.
- A line is a straight path of points that extends infinitely in two opposite directions. It has one dimension (length) but no width.
- A plane is a flat, two-dimensional surface that extends infinitely. It has length and width but no thickness.
2. Why are 'point', 'line', and 'plane' considered undefined terms in geometry?
Point, line, and plane are considered undefined terms because they are so fundamental that they cannot be defined using other, simpler geometric terms. Instead of a formal definition, we rely on a shared, intuitive understanding of what they are. They serve as the foundational concepts, or 'primitive concepts', upon which the definitions of all other geometric figures and theorems are built.
3. What is the main difference between collinear and coplanar points?
The main difference lies in the geometric element they share. Collinear points are a set of points that all lie on the same single straight line. In contrast, coplanar points are a set of points that all lie on the same flat surface, or plane. While any two or three collinear points are always coplanar, four or more coplanar points are not necessarily collinear.
4. How can you differentiate between parallel, intersecting, and perpendicular lines?
These types of lines are differentiated by how they are positioned relative to each other in a plane:
- Parallel lines are two lines on the same plane that never cross or meet, no matter how far they are extended. They always maintain the same distance from each other.
- Intersecting lines are two lines that cross each other at exactly one common point.
- Perpendicular lines are a special type of intersecting lines that cross at a right angle (90 degrees).
5. Can you provide some real-world examples that represent a point, a line, and a plane?
Yes, we can find representations of these geometric concepts all around us:
- Point: The tip of a pen, a specific star in the sky, or a corner of a box can all represent a point.
- Line: A stretched-out string, the edge of a ruler, or a railway track extending into the distance are good representations of a line or line segment.
- Plane: The surface of a table, a wall, the screen of a phone, or the surface of a calm lake are all examples that model a plane.
6. If a point has zero dimensions, how can a collection of points form a line, which has one dimension?
This is a foundational concept in geometry. While a single point has no dimension, a line is understood as an infinite set of points placed so densely next to each other that they create a continuous path with one dimension: length. The dimension doesn't come from the points themselves but from the continuous arrangement and extension of these points in a specific direction. It's the 'betweenness' and continuity of the points that give a line its length.
7. Are all collinear points also coplanar? Explain why.
Yes, any set of collinear points is always coplanar. This is because if a set of points lies on a single straight line, you can always find a plane (in fact, infinitely many planes) that contains that entire line. Think of a line as the spine of an open book; each page represents a different plane passing through that same line (the spine). Therefore, any points on that line must also lie on any of those planes.























