




How to Solve Multiplicative Comparison Problems in Maths
Multiplication is a key maths topic that requires a basic understanding of operations as well as problem-solving abilities. Multiplicative comparison is a good way of understanding the fundamentals of multiplication. We will examine multiplicative comparison in this article, which will reinforce knowledge of this important topic and improve your confidence in solving long multiplication comparisons.
What is Multiplicative Comparison?
A multiplicative comparison compares two quantities such that when one is multiplied by a certain number, the other is produced.
A statement that compares two sets of items will lead to a multiplication equation in multiplicative comparison problems. The unknown quantity could be represented by a symbol or a letter in the equation.
With multiplicative comparison you can:
Explain how multiplication can be used to compare quantities.
Write equations to show multiplicative comparison.
Know how multiplicative comparisons are represented (bar models can help students in visualising the different types of comparisons and connecting them to the relationship between multiplication and division).
Explain the difference between multiplicative and additive comparisons.
Terminology
A multiplicative comparison implies the relationship between two values by multiplying one of them by a constant. To compare the values of the two quantities, words like "twice" or "triple" are frequently used. The phrase "Ram spent twice as much as Shyam," indicates that the relationship between both has a multiplicative value of 2.

An Example Explaining the Terminology of Multiplicative Comparison.
Problems involving multiplicative comparison have phrases like:
Times as many (Arjun has 4 times as many coins as Tara).
Times as much (My brother travels 3 times as much as I do for a job).
Times as long (This area is 3 times as long as the previous one).
Times the height (The tower is 2 times the height of the tree).
How to Solve Problems Based on Multiplicative Comparison?
When given a word problem that needs a multiplicative comparison, solve it as follows:
Get an equation with two unknowns that represents the multiplicative comparison.
Determine the value of one of two unknowns from the equation.
Assign the known value into the equation and solve for the other unknown value.
Example:
1. Ram’s family spends Rs 2500 every week on groceries and Shyam’s family has a budget that is triple Ram's budget. How much do the Shyam spend on groceries each week?
Sol: We will first write an equation relating Ram's budget (R) with Shyam's budget (S). Since the problem has the word "triple", we understand that Shyam's budget is 3 times more than Ram's budget.
Now, We can write this as an equation, S = 3 × R
From the word problem, we can determine that Ram's budget is 2500 Rs.
Let’s substitute the value of R to the equation, S = 3 × 2500
Calculating this equation using multiplication, we get: S = 7500 Rs
Shyam’s weekly grocery budget is Rs 7500.
2. Two racers race up a 1000-metre race. When racer A gets to the last point, racer B's forward progress is one-fifth of racer A's. How far up did racer B get before the race was won?
Sol: We will write an equation relating racer B's progress to racer A. Since racer B's progress is smaller than racer A's, we will write the equation with the fractional multiplier applied to racer A:
B = 1/5 × A
The word problem statement indicates that racer A won the race by ascending the entire track. Therefore, at the end of the race, racer A's progress is 1000 metres, which implies A = 1000
We can now plug this value into the equation which we wrote earlier to find racer B's progress, once racer A reaches the end.
B = 1/5 × 1000 = 1000/5 = 200
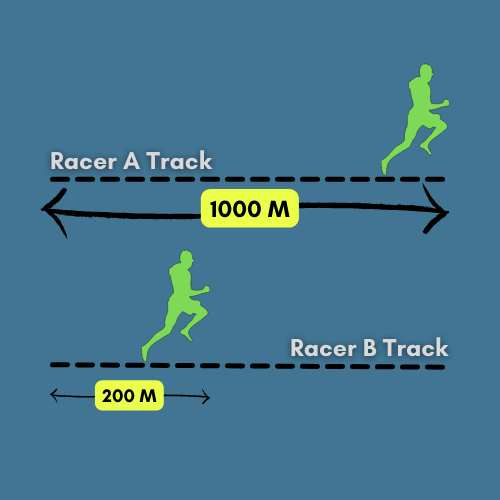
Comparing Two Racers on a Track
Therefore, racer B had reached 200 metres of the track when racer A just finished the race.
Conclusion
Multiplicative comparisons compare two quantities by showing that one quantity is a certain number of times larger or smaller than the other. The situations require a multiplicative comparison, which means they must be able to multiply or divide to find an unknown value.
FAQs on Multiplicative Comparison Explained: Key Concepts & Examples
1. What are the three types of multiplicative comparison problems?
There are three types of multiplicative comparisons:
When the number being compared is unknown.
When the number being compared to, is the unknown.
When the multiplier is unknown.
Students are challenged in this article to understand the problem situation, model it, identify or write equations to tell what is happening in the problem, and solve it.
2. How does place value help me multiply numbers?
You have studied multiplication as repeated addition. For example, it is nothing but thinking of 3 groups of 5 as 5 + 5 + 5. This is additive thinking, but multiplication is more than just repeated addition. This can represent comparisons in which one set or quantity is defined in terms of another through the use of multiplicative thinking. The examples for the same are discussed in detail in the above article.























